Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 48

48. O homem puxa a corda a uma taxa constante de 0,5 m/s. Determine a velocidade angular e aceleração angular da viga AB quando θ = 60 ° . A viga gira em torno de A. Despreze a espessura da viga e a dimensão da polia.

Passo 1

Para resolver está questão basta utilizar as equações e raciocínios desenvolvidos ao longo dessa seção inicial do capitulo 16. Seria importante também antes de começar a resolver as questões problemas, fazer as 6 questoes fundamentais pois de alguma forma a resolução delas ajudará em praticamente todas as resoluções. Pois, cada questão problema estará relacionada com algum conceito de alguma questão fundamental.

Passo 2

Um esboço do que foi dito no enunciado pode ser representado por:

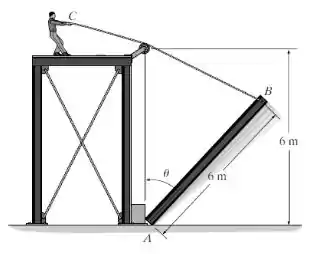
Passo 3

Aplicando a lei dos cossenos no esboço para obter a posição como função do ângulo vem:

s 2 = 6 2 + 6 2 - 2 6 6 cos ⁡ θ

s 2 = 72 - 72 c o s θ m 2

Derivando a expressão com relação ao tempo, teremos:

2 s d s d t = 0 + 72 s e n θ d θ d t

s d s d t = 36 s e n θ d θ d t                 ( 1 )

Quando θ = 60 ° ,   s = 72 - 72 c o s 60 ° = 6 m e d s d t = - 0 , 5 m s podemos substituir na equação:

6 - 0 , 5 = 36 s e n 60 °   ω

ω = - 0,0962   r a d / s

Passo 4

Derivando com relação ao tempo a expressão (1), temos:

s d 2 s d t 2 + d s d t 2 = 36 s e n θ d 2 θ d t 2 + c o s θ d θ d t 2    

Como d 2 s d t 2 = 0   quando θ = 60 ° podemos substituir:

6 0 + - 0,5 2 = 36 s e n   60 °   α + cos ⁡ 60 ° - 0,0962 2

α = 0,00267   r a d / s 2

Resposta

ω = - 0,0962   r a d / s

α = 0,00267   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pequena braçadeira de massa mB está presa em B a um arco de massa mh. Sabendo que o sistema é liberado a partir do repouso e rola sem deslizar, deduza uma expressão para a aceleração angular do ar
A metade da seção do cilindro uniforme de massa m está em repouso quando a força P é aplicada como mostra a figura. Considerando que a seção rola sem deslizamento, determine (a) sua aceleração angular
Uma barra de 2 kg é ligada a um cilindro uniforme de 5 kg por um pino quadrado P, como mostrado na figura. Sabendo que r = 0,4 m, h = 0,2 m, θ = 20°, L = 0,5 m eω = 2 rad /s no instante mostrado, dete
As extremidades da haste uniforme AB de 2 kg são presas a cursores de peso desprezível que deslizam sem atrito ao longo de hastes fixas mostradas na figura. Se haste AB é liberada do repouso na posiçã
O movimento da haste uniforme AB de massa 5 kg e comprimento L = 750 mm é guiado por pequenas rodas de massa desprezível que rolam sobre a superfície mostrada na figura. Se a haste é liberada a partir