Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 104
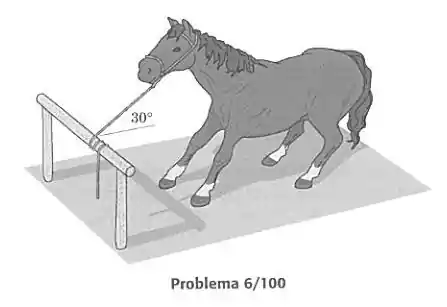
Em filmes do Velho Oeste, frequentemente se observa os caubóis prendendo seus cavalos simplemente dando poucas voltas da rédea em torno de uma barra horizontal e deixando a extremidade pendendo livremente como mostrado – sem nós! Se o comprimento pendurado da rédea tem uma massa de 0,060 kg e o número de voltas é como mostrado, que força trativa o cavalo deve fazer na direção mostrada, para se libertar? O coeficiente de atrito entre a rédea e a barra de madeira vale 0,70.
Passo 1
Para que a corda escorregue e o cavalo consiga se soltar, a força que ele faz deve superar o peso da corda pendurada e a força de atrito entre a corda e a barra. No limiar do escorregamento, ou seja, quando a corda está prestes a escorregar, a corda está em equilíbrio e a equação para a corda é:
Sendo e as trações maior e menor nas extremidades da corda, o coeficiente de atrito entre a corda e a superfície e o ângulo total de giro da corda. Através dessa fórmula, seremos capazes de achar a força .
Passo 2
A tração menor na corda é claramente o peso do trecho pendurado. Como sua massa é de 0,060 kg, multiplicamos pela aceleração da gravidade e obtemos :
O que queremos é achar a tração maior . Temos o coeficiente de atrito e devemos contar as voltas da corda na barra para determinar o ângulo total .
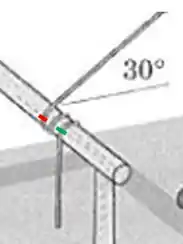
Olhando a figura, se começarmos a contar a partir do traço verde temos até o vermelho duas voltas, e ainda falta uma parte. A outra parte corresponde a um ângulo de , como mostra a figura:
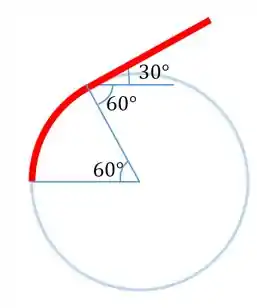
Então o ângulo total é duas voltas mais :
Passo 3
Agora só falta substituir os valores na fórmula:
Para acharmos passamos a fórmula para a forma exponencial: