Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 35

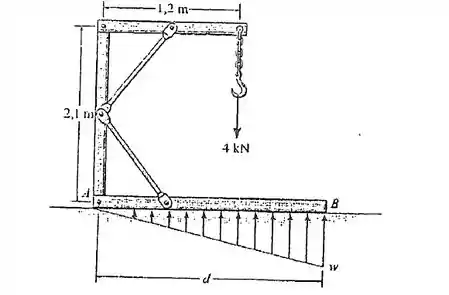
5.35. A estrutura é sustentada pelo membro AB, que está apoiado sobre o piso liso. Quando carregada, a distribuição de pressão sobre AB é linear, como mostra a figura. Determine o comprimento do membro AB e a intensidade para esse caso.

Passo 1

Faalaa! A gente quer e . Mas vamos entender o que está acontecendo. Temos essa estrutura aí criativa. A reação dela é dada por todo membro , e ela tem esse formato de carga distribuída. Algo assim:

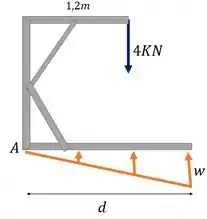
Para a gente consegui trabalhar com essa estrutura, vamos substituir essa carga distribuída por uma concentrada equivalente. Como assim? A intensidade da força vai ser a área desse triângulo da carga distribuída, assim:

E a posição vai ser a coordenada do centroide desse triângulo. O centroide do triângulo é 1/3 da base, então ficamos assim:

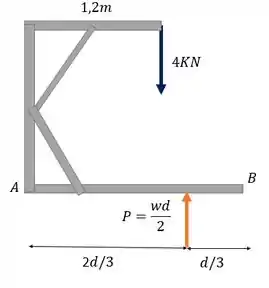
Vamos aplicar as condições de equilíbrio, ou seja, a força resultante tem que ser 0, tal como o momento, nessa nova estrutura equivalente, e achar o que ele pede. Bora!

Passo 2

Vamos começar com a resultante das forças no eixo y

Passo 3

Agora vamos usar a proposição que somatória do momento é 0, para determinar a distância .

Vamos calcular o somatório dos momentos no ponto , considerando o sentido anti-horário positivo. Aqui cê pode esquecer o formato da estrutura e só olhar para o sentido e posição das forças e do ponto :