Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 41
5.41. Determine as componentes horizontal e vertical da reação no pino A e a reação do colar liso B sobre a barra.
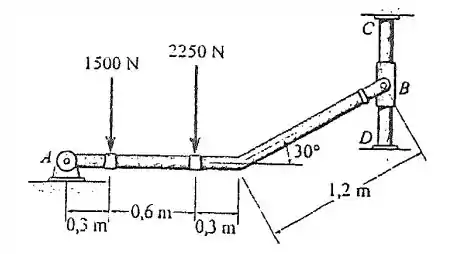
Passo 1
Beleza, como o sistema está estático, podemos dizer que
Então
Passo 2
Agora vamos usar a equação de equilíbrio ao longo do eixo y
Logo
Passo 3
E finalmente vamos usar a equação de equilíbrio ao longo do eixo x
Logo
Resposta
Exercícios de Livros Relacionados
7.17. Sabendo que o raio de cada roldana é 200 mm e desprezando o atrito, determine as forças internas no ponto J da estrutura mostrada na figura.
7.15. Sabendo que o raio de cada roldana é 150 mm, que α = 20 ° e desprezando o atrito, determine as forças internas em (a) no ponto J, (b) no ponto K
7.13. Uma barra semicircular é carregada tal como mostra a figura. Determine as forças internas no ponto J sabendo que θ = 30 °
7.18. Sabendo que o raio de cada roldana é 200 mm e desprezando o atrito, determine as forças internas no ponto K da estrutura mostrada na figura.
7.14. Uma barra semicircular é carregada tal como mostra a figura. Determine a intensidade e a localização do momento fletor máximo na barra.