Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 17

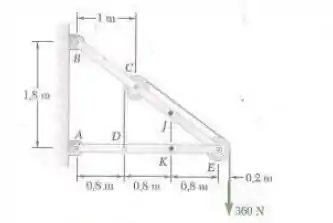
7.17. Sabendo que o raio de cada roldana é 200 mm e desprezando o atrito, determine as forças internas no ponto J da estrutura mostrada na figura.

Passo 1

Vamos começar desenhando a situação

Bem, daqui a gente já pode tirar as forças de reação em A e B, só usando as equações de equilíbrio, primeiro vamos fazer o momento em A.

∑ M A = 0

- B x ⋅ 1,8 - 360 ⋅ 3 ⋅ 0,8 + 0,2 = 0

Então

B x = - 520   N

Agora vamos usar as forças

∑ F x = 0

A x - 520 = 0

Logo

A x = 520

Agora em y

∑ F y = 0

A y + B y - 360 = 0

A y + B y = 360

Bem não conseguimos definir as forças em y ☹, mas vamos fazer isso ainda, no próximo passo.

Passo 2

Agora vamos usar o corpo livre no membro A E - , para determinar A y

Aquela força ali no ponto D é por causa da roldana, a tensão no cabo em cima do ponto D é de 360   N .

Agora vamos usar o momento em E para determinar A y

∑ M E = 0

- A y ⋅ 2,4 - 360 ⋅ 1,6 = 0

Logo

A y = - 240   N

E como

A y + B y = 360

Então

B y = 360 + 240

B y = 600   N

Passo 3

Agora vamos fazer as forças internas, para isso vamos usar o membro B J -

Lembrando que qualquer força aplicada numa roldana a gente aplica direto no eixo.

Vamos usar as equações de equilíbrio, mas vamos precisar decompor as forças nas novas coordenadas x’ e y’. Vamos usar esse triângulo para ajudar a gente.

Vamos calcular a hipotenusa

h = 1,2 2 + 1,6 2 = 2

Então sabemos que

cos ⁡ θ = 1,2 2

sin ⁡ θ = 1,6 2

Agora a gente calcula

∑ F y ' = 0

1,2 2 600 + 1,6 2 520 - 360 - 1,2 2 360 - F = 0

Então

F = 200

Agora o esforço cortante

∑ F x = 0

1,6 2 600 - 1,2 2 520 - 1,6 2 360 + V = 0

Logo

V = 120   N

Agora só falta o momento fletor, vamos usar o momento no ponto J

∑ M J = 0

520 ⋅ 1,2 - 600 ⋅ 1,6 + 320 ⋅ 0,6 + M = 0

Logo

M = 120   N ⋅ m

Resposta

F = 2 00   N

V = 12 0   N

M = 120   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.115. Se uma força P = 100N é aplicada no cabo do grampo articulado, determine a força de prensagem horizontal N E que o grampo exerce sobre o bloco liso de madeira em E.
6.109. Se uma força de prensagem de 300N é necessária em A, determine a quantidade de força F que precisa ser aplicada no cabo do grampo articulado.
Se o bloco de madeira exerce uma força de F = 600 N sobre o grampo, determine a força P aplicada no cabo do grampo.
Se P = 75 N , determine a força F que o grampo exerce sobre o bloco de madeira.
Os ganchos são usados para suspender a placa lisa de 500k g . Determine a força de compressão resultante que o gancho exerce sobre a placa em A e B , e a reação do pino em C .