Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 45
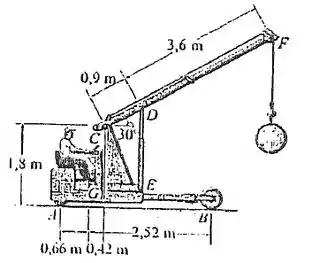
5.45. A grua de chão e o operador possuem um peso total de com um centro de gravidade em G. Se a grua precisa suspender o tambor de , determine a reação normal em ambas as rodas em A e ambas as rodas em B quando a lança está na posição mostrada.
Passo 1
Fala, querido! Queremos as reações em e .
Aqui temos um sistema estático. Olha nosso DCL:
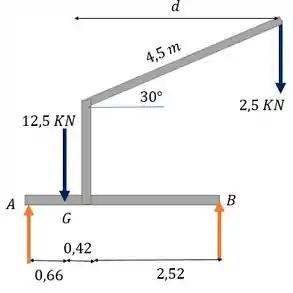
Só estamos de olho nas reações normais, então vamos esquecer o eixo e fazer as equações de equilíbrio de forças em e momentos.
Bora!
Passo 2
Beleza, como o sistema está estático, podemos dizer que
Vamos considerar o anti-horário como positivo. Mas repara uma coisa, o braço de alavanca da força de é
Essa é a distância entre a linha vertical que passa por e a linha de ação da força.
Mas quem é ? Cara, ele é a projeção dessa distância inclinada no eixo . Podemos achar assim:
Aí finalmente, nosso somatório de momentos fica:
Então
Passo 3
Agora vamos usar a equação de equilíbrio ao longo do eixo y
Logo