Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 8
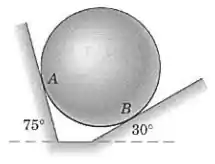
A esfera lisa e homogênea de está apoiada nos dois planos inclinados como mostrado. Determine as forças de contato em e .
Passo 1
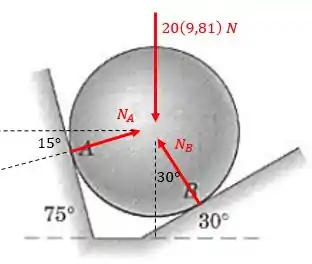
As forças de contato e devem ser perpendiculares às suas respectivas superfícies. Sendo assim, essas forças juntamente com o peso da esfera podem ser representados na figura a seguir:
Passo 2
De acordo com os ângulos da figura, escrevemos a equação de equilíbrio de forças na horizontal:
Vamos isolar , pois será útil mais tarde:
Passo 3
Agora, escrevemos a equação de equilíbrio de forças na vertical:
Vamos substituir a expressão de para determinar :
Por último, determinamos :
Resposta
Exercícios de Livros Relacionados
Um torque de 24Nm é necessário para girar o parafuso em torno de seu eixo. Determine P e as forças entre as paredes endurecidas e lisas da chave e os vértices A e B da cabeça hexagonal do parafuso. Co
Uma parte do mecanismo de troca de marcha para um carro com transmissão manual está mostrada na figura. Para a força de 8N exercida na alavanca de câmbio, determine a força P correspondente exercida p
Estime a força F necessária para levantar do chão os pneus traseiros do carro de corrida. Você pode assumir que a parte C D do macaco é horizontal. A massa combinada do carro e do motorista é 700k g c
Determine o momento M que deve ser aplicado ao eixo de forma a manter o hemisfério homogêneo em uma posição angular arbitrária, medida pelo ângulo θ . Os raios das engrenagens A , B e do hemisfério sã
É desejável que uma pessoa seja capaz de iniciar o fechamento da porta do bagageiro de uma van, desde a posição aberta mostrada, com uma força vertical P de 40N . Como um exercício de projeto, determi