Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 23

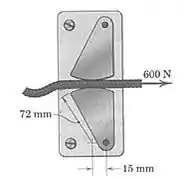
6/23) A figura mostra um dispositivo , chamado presilha de travamento , que prende uma corda sob tração devida às grandes forças de atrito desenvolvidas . Determine , para a posição mostrada , o coeficiente mínimo de atrito estático μ s entre a corda e as superfícies do came , para o qual a presilha será autotravante. Encontre também o módulo da reação total R em cada um dos mancais do came .

Passo 1

Então galera , como já foi demonstrado neste capítulo e em exercícios anteriores , o coeficiente mínimo de atrito é dado por :

μ s = tan ⁡ θ

Onde θ é o ângulo formado entre o força de atrito e o eixo horizontal.

Sendo assim , o coeficiente mínimo de atrito nesse caso é obtido pela relação :

μ s = tan ⁡ ∅ = tan ⁡ θ = 15 72 = 0,208

Passo 2

Bom pessoal , agora para resolvermos este exercício será preciso aplicar a equação de equilíbrio da corda em relação ao eixo x .

Sendo assim , nós temos que :

∑ F = 0

2 R sen ⁡ θ = 600

R = 300 15 / 15 2 + 72 2 = 1471   N  

Resposta

μ s = 0,208

R = 1471   N  

Suave galera? Então bora próxima!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro de massa 250k g deve ser suportado pela corda que envolve o cano. Determine a maior força vertical F que pode ser aplicada à corda sem mover o cilindro. A corda passa (a) uma vez pelo cano
O barco tem um peso de 2500N( ≈ 250k g ) e é mantido na posição lateral de um navio pelas vergas em A e B . Um homem com um peso de 650N( ≈ 65k g ) entra no barco, enrola uma corda em torno de uma lan
Um cilindro de massa 250k g deve ser suportado pela corda que envolve o cano. Determine a menor força vertical F necessária para suportar a carga se a corda passa (a) uma vez pelo cano, β = 180 ° e (b
Os blocos A e B pesam 375N cada, e D pesa 150N . Usando os coeficientes de atrito estático indicados, determine a força de atrito entre os blocos A e B e entre o bloco A e o piso C .
Os blocos A e B pesam 250N e 150N , respectivamente. Usando os coeficientes de atrito estático indicados, determine o maior peso do bloco D sem causar movimento.