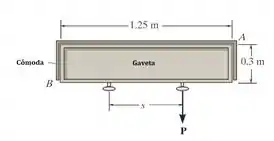
Uma única força é aplicada ao puxador da gaveta. Se o atrito for desprezado no fundo e o coeficiente de atrito estático for , determine o maior espaçamento entre os puxadores simetricamente posicionados de modo que a gaveta não prenda nos cantos e quando a força for aplicada a um dos puxadores.
Passo 1
De início, vamos dar uma olhada no diagrama de corpo livre dessas questão para entendermos as forças que estão atuando.
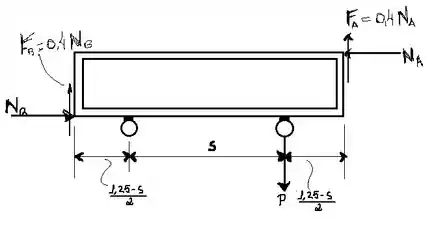
Passo 2
Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:
Passo 3
O somatório dos momentos em relação a um ponto, para o sistema em equilíbrio, deve ser igual a zero. Vamos calcular o momento em relação ao ponto e, assumindo como sentido positivo o anti-horário, temos:
Como não queremos que (se for zero quer dizer que não há contato com a cômoda), nos resta fazer que :
Resposta
O maior espaçamento entre os puxadores simetricamente posicionados de modo que a gaveta não prenda nos cantos e é igual a: