Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 17

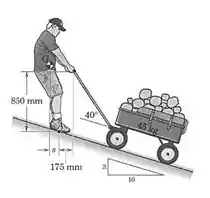
6/17) Um homem de 82   k g puxa um carrinho de 45   k g para cima na rampa a velocidade constante . Determine o coeficiente de atrito estático mínimo μ s para o qual os sapatos do homem não escorregarão . Determine também a distância s necessária para o equilíbrio do corpo do homem .

Passo 1

Então galera , a primeira coisa que devemos fazer é calcular o ângulo de inclinação da rampa através da relação :

α = tan - 1 ⁡ 3 10 = 16,7 °

Agora tudo fica mais fácil . Aplicando a equação de equilíbrio em relação ao carrinho , temos que :

∑ F x = 0

- T cos ⁡ 40 ° + 100 sen ⁡ α = 0

Logo ,

T cos ⁡ 40 ° = 100 sen ⁡ 16,7 °

T = 100 sen ⁡ 16,7 ° cos ⁡ 40 ° = 37,5   l b

Passo 2

Bom pessoal , aplicando as equações de equilíbrio que conhecemos ( em relação aos eixos x e y e ao momento em relação a A ) obtemos que :

∑ F x = 0   :   - F + 180 sen ⁡ α - 37,5 sen ⁡ 40 ° = 0

F = 37,5 sen ⁡ 40 ° - 180 sen ⁡ 16,7 °

Logo ,

F = 80,5   l b

∑ F y = 0   :   N - 180 cos ⁡ α - 37,5 sen ⁡ 40 ° = 0

N = 180 cos ⁡ 16,7 ° + 37,5 sen ⁡ 40 °

Sendo assim ,

N = 196,6   l b

Passo 3

Utilizando os resultados obtidos no passo anterior , podemos calcular coeficiente de atrito estático mínimo μ s através da relação :

F = μ S N

Logo , temos que :

μ s = F N = 80,5 196,5 = 0,409

Analisando o momento em relação a A , achamos que :

∑ M A = 0  

180 s - 37,5 cos ⁡ ( α + 40 ° ) 34 - 37,5 sen ⁡ α + 40 ° 7 = 0

Sendo assim ,

s = 5,11   i n

Resposta

μ s = 0,409

s = 5,11   i n

De boa galera? Então bora resolver mais exercícios como esse!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Antes de correr, um corredor alonga as panturrilhas se inclinando contra uma parede, como mostrado na figura. Essa posição é atingida sem força vertical (atrito) entre suas mãos e a parede. Qual é o c
O bloco de 80 kg está colocado contra a mola em um plano com inclinação de 20° e é solto a partir do repouso. O coeficiente de atrito estático entre o bloco e o plano inclinado vale 0,25. ( a ) Determ
Um dispositivo de travamento por atrito permite que a barra A se mova para a esquerda, mas previne movimento para a direita. Se o coeficiente de atrito entre a sapata B e a barra A vale 0,40, especifi
Três caixas em contato entre si são colocadas em um plano inclinado e são soltas a partir do repouso. Os coeficientes de atrito estático sob as caixas A , B e C valem 0,30, 0,20 e 0,35, respectivament
O disco homogêneo de massa m está em repouso sobre as superfícies de apoio em ângulo reto mostradas. A força trativa P na corda é aumentada bem gradualmente desde zero. Se o atrito, tanto em A quanto