Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 25

Uma janela corrediça pesando 50 N é geralmente sustentada por dois pesos de 25 N. Sabendo que a janela permanece aberta depois que uma das cordas dos pesos foi cortada, determine o menor valor possível do coeficiente de atrito estático. (Considere que os pesos são levemente menores que a estrutura e se prenderão apenas nos pontos A e D.)

Passo 1

Beleza! Vamos começar esse excercício desenhando o DCL para a janela:

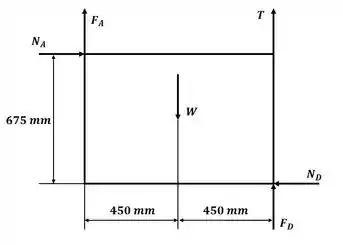
Passo 2

Conforme dito no enunciado, como a janela é sustentada por dois pesos de 25 N, temos que:

Agora, sabemos também que as forças de atrito em A e D podem ser escritas como:

Passo 3

Agora, aplicando o somatório de forças na direção :

Agora vamos aplicar o somatório de momento em relação ao ponto D:

Agora aplicando o somatório de forças na direção :

Agora, substituindo as expressões de e encontradas no passo 1:

E, conforme vimos, , então:

Substituindo o valor de :

Então, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro D de 10k g , que está preso a uma pequena polia B , é colocado na corda conforme a figura. Determine o maior ângulo θ de modo que a corda não deslize pelo pino em C . O cilindro em E tem u

Se uma força P = 200N é aplicada ao cabo da alavanca em L , determine o torque máximo M que pode ser resistido de modo que o volante não esteja na iminência de girar no sentido horário. O coeficiente

Um fazendeiro de 90k g tenta evitar a vaca escape enrolando a corda com duas voltas em torno do tronco da árvore, como mostra a figura. Se a vaca exerce uma forca de 125N sobre a corda, determine se o

Um homem de 80k g tenta baixar a caixa de 150k g usando uma corda que passa por um pino rugoso. Determine o menor número de voltas além da volta básica ( 165 ° ) em torno do pino para realizar o traba

Mostre que a relação de atrito entre as trações na correia, o coeficiente de atrito μ e os contatos angulares α e β para a correia V é T 2 = T 1 e μ β s e n α 2