Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 33
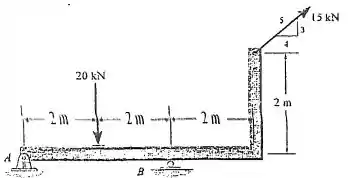
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro medida a partir de .
Passo 1
Oi, tá bem? Torço para que sim!
A questão pede para substituirmos o sistema de forças por uma única força resultante e especificar em que ponto essa força age. Como se trata se um sistema de forças coplanares (contidas num mesmo plano), é possível fazer essa redução sem precisar adicionar um binário resultante também.
Segue esse passo a passo que vamos seguir, que dá bom!
O primeiro passo é calcular a força resultante, essa vai ser nossa força equivalente para todo o sistema de forças.
Vamos usar a forma vetorial, porque por ela é mais tranquilo de fazer somatório de vetores. Repara que temos a força . Como ela está para baixo, ela só terá uma componente negativa em . Aí o vetor dela é
Para , temos que seguir a inclinação dada pelo triângulo retângulo. Como o lado que vale está paralelo a , a componente horizontal da força vale . A componente vertical vai valer , porque o lado que vale é paralelo a . Ambas estão nos sentidos positivos dos eixos.
Colocando isso num vetor
Somando as duas forças, componente a componente
Assim,
Passo 2
O segundo passo é calcular o momento de binário resultante. Por que? Porque a gente precisa encontrar a posição de que vai causar um momento equivalente a ele. Então precisamos desse momento resultante.
Vale lembrar que o momento de uma força com relação ao ponto é dado por
Onde é o vetor que sai do ponto em relação ao qual queremos o momento e vai para o ponto de aplicação da força.
Podemos escolher calcular o momento em relação a , a origem. Como , as componentes dos vetores vão ser numericamente iguais às coordenadas dos pontos de aplicação da força.
Assim, o momento resultante com relação ao ponto será a soma dos momentos de cada força
Assim,
Portanto,
Passo 3
Para finalizar, precisamos achar o ponto que a força resultante deve ser aplicada para compensar esse momento resultante. Esse vai ser o ponto onde a linha de ação dessa resultante intercepta o membro a partir de
Já achamos a força resultante do sistema e momento resultante. Agora queremos a posição dessa força para que ela gere o momento resultante, o que podemos equacionar assim:
Podemos supor que a força vai estar localizada na parte horizontal do membro distante de . Para esse ponto de aplicação, temos e . O vetor que sai de (a origem) e vai até esse ponto de aplicação de vai ser
Assim,
Assim, a força resultante deve ser aplicada a uma distância do ponto .