Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 81
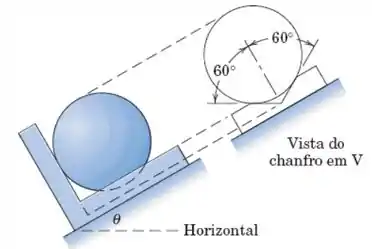
A esfera lisa e homogênea repousa na cantoneira de e se apoia contra a placa, que é normal à direção da cantoneira. Determine o ângulo , medido a partir da horizontal, para o qual a reação em cada lado da cantoneira é igual à força suportada pela extremidade da placa.
Passo 1
Primeiro precisamos entender o que o ângulo tem a ver com a força suportada pela placa e pela canaleta. Imagine que o ângulo fosse . Nesse caso, o suporte estaria na horizontal, e não haveria força contra a parede. Então beleza, já entendemos que controla a distribuição de forças entre a canaleta e a parede. Vamos dar nome à essas forças e determinar os eixos e os ângulos
Passo 2
Ok, agora podemos começar a aplicar equações de equilíbrio. Vamos considerar o equilíbrio das forças em cada direção
Dê uma olhada no nosso desenho para descrever as expressões para as forças em cada direção
Lembre que estamos procurando o caso em que as forças nos dois lados da canaleta e na placa são iguais, então, vamos chamar tudo por um mesmo nome
E ficamos com o seguinte sistema
Simplificando ficamos com
Dividindo uma equação pela outra vamos ter
Pronto, tá resolvido nosso problema.
Resposta
Ei, a resposta está no passo a passo :)