9.94 O tanque de parede fina é fabricado a partir de um hemisfério e de uma casca cilíndrica. Determine as reações verticais que cada uma das pernas posicionadas simetricamente exerce sobre o solo se o tanque contém água, que está a de profundidade no tanque. A gravidade especifica da água é de . Despreze o peso do tanque.
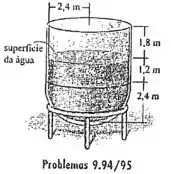
Passo 1
As pernas vão suportar somente o peso da água, já que devemos desprezar o peso do tanque. Como já temos sua gravidade especifica, só precisamos do volume de água. Esse volume pode ser gerado a partir da revolução de duas áreas:
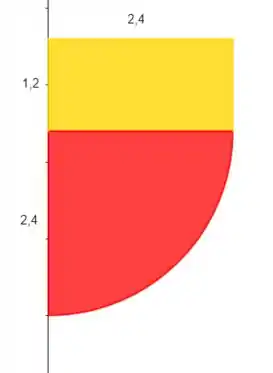
A área amarela é retangular e a vermelha é um quarto de um circulo. Perceba que nós só pegamos a área necessária para calcular o volume de água e não o volume do tanque inteiro.
A fórmula para determinar o volume é:
Onde é o ângulo de revolução em radianos, nesse caso
é a distância perpendicular do eixo de revolução ao centroide da área de geração. O centroide de um retângulo fica bem no meio dele, então
E o centroide de um quarto de circulo é tabelado, ele vai ficar:
E é a área de geração, ou seja a área de cada formato:
e
Passo 2
Então é só aplicar na formula e obteremos o volume:
Para descobrirmos o peso da água precisamos multiplicar seu volume pela sua gravidade espcifica:
Esse então é o peso total, como tem quatro pernas posicionadas simetricamente essas pernas dividiram o peso da água igualmente entre ela, então a força suportada por cada perna será: