Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas - Ex. 91
9.93 O alimentador está cheio até o topo com carvão. Estime o volume do carvão se os vãos (espaço vazio) correspondem a 35% do volume do alimentador.
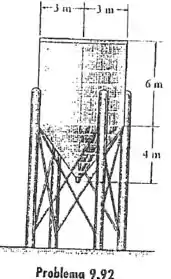
Passo 1
Para calcular o volume, vamos separar o sólido em um triângulo e dois retângulos, para fazer a revolução deles:
A fórmula para determinar o volume é:
Onde é o ângulo de revolução em radianos, nesse caso
é a distância perpendicular do eixo de revolução, nesse caso o eixo , ao centroide da área de geração. O centroide de um retângulo fica bem no meio dele, então
E o centroide de um triângulo é tabelado, ele vai ficar:
E é a área de geração, ou seja a área de cada formato.
O retângulo amarelo:
O retângulo azul:
O triângulo vermelho:
Passo 2
Então é só aplicar na formula e obteremos o volume:
Como 35% do reservatório contem espaços vazios, sobra 65% de espaços com carvão. Logo o volume de carvão no reservatório vai ser de: