Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 96
9.96 Determine a área da superfície do tanque, que consiste em um cilindro e uma tampa hemisférica.
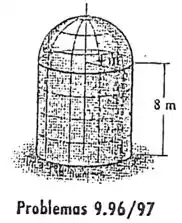
Passo 1
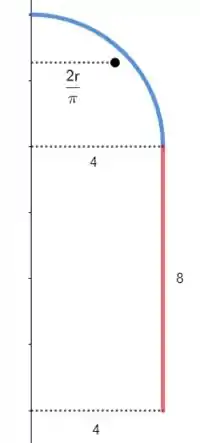
Para gerarmos essa superfície devemos fazer a revolução de 1 segmento de reta e um quarto de circunferência:
A fórmula para determinar a área superficial é:
Onde é o ângulo de revolução em radianos, nesse caso
é a distância perpendicular do eixo de revolução ao centroide da curva de geração.
O centroide de uma segmento de reta fica sempre no seu centro, então nesse caso é a própria distância do eixo até a reta:
E o centroide de um quarto de circunferência é tabelado:
E é o comprimento da curva de geração, nós já sabemos o tamanho de:
E o comprimento de m quarto de circunferência é:
Passo 2
Agora é só aplicar na fórmula:
Resposta
Exercícios de Livros Relacionados
O corpo mostrado em seção transversal é a metade de um anel circular obtido pela revolução de 180 graus da área sombreada em torno do eixo z . Determine a área superficial A do corpo.
Calcule o volume V do anel que tem a seção transversal mostrada.
Determine o volume V gerado pela revolução de 90 graus em torno do eixo z da área em forma de quarto de circulo.
A área mostrada é girada de 360 graus em torno do eixo y . Determine o volume do corpo resultante, que é uma esfera que tem uma parte significativa removida.
O tanque de armazenamento de água é uma casca de revolução e deve ser recoberto duas camadas de tinta, que dá uma cobertura de 16m 2 por galão. O engenheiro (que se lembra de mecânica) consulta um des