Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 96
96- A fim de obter a melhor distribuição de peso sob as quatro rodas da caminhonete de carga do Problema , um tipo de fixação compensatória mostrada na figura é usada para a caminhonete rebocar o trailer. A fixação consiste em duas barras amortecedoras (apenas uma é mostrada na figura) rigidamente encaixadas em rolamentos dentro do suporte preso junto a caminhonete. As barras são também conectadas por correntes na estrutura do trailer, e ganchos especialmente projetados tornam possível colocar ambas as correntes em tração
Determine a tensão necessária em cada uma das correntes se o carregamento adicional do trailer for uniformemente distribuído sobre as quatro rodas da caminhonete
Quais são as reações resultantes em cada uma das seis rodas da combinação trailer- caminhonete.
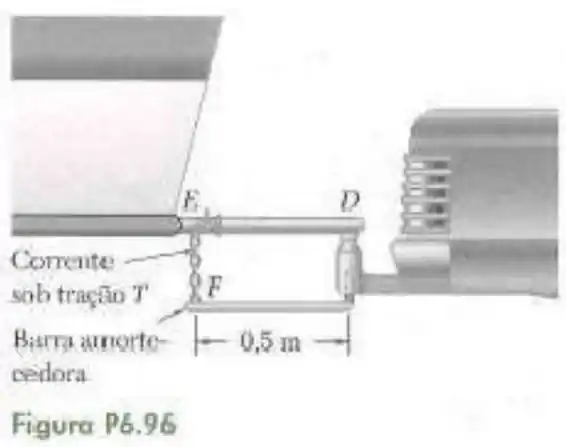
Passo 1
Essa questão te dá muita informação mas basicamente ele diz que esse mecanismo esquisito novo aí faz com que o peso do trailer seja igualmente distribuído entre as rodas da caminhonete (ou picape, é a mesma coisa) e para isso vamos desenhar o diagrama de forças somente considerando a influência do peso do trailer.
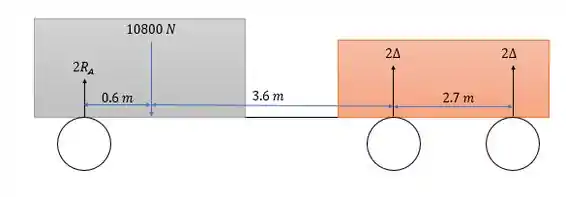
Os valores de e da questão passada surgem por conta do peso do carro, se ignorarmos isso e focarmos somente na influência do peso do trailer nós teremos as variações que nessa questão são iguais por conta do mecanismo proposto.
Por ação e reação as forças e se anulam quando vemos as forças no corpo todo.
Agora se fizermos a somatória dos momentos em nós vamos ter.
A reação em nós encontramos pela somatória de todas as forças.
Pode até se fazer analisando primeiro o trailer e depois a caminhonete mas poderia ser confundir os pois é causado somente pela influência do peso do trailer.
Passo 2
E isolando o carro (ainda considerando somente a influência do trailer, pois é graças a ele que surge a força nas duas correntes) nós teremos o seguinte diagrama de forças.
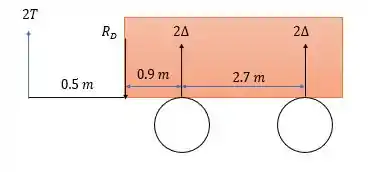
Fazendo a somatória dos momentos em temos:
Isso responde a letra a.
Passo 3
Da questão passada encontramos a reação em repouso nas duas rodas.
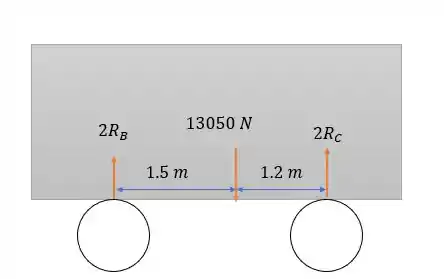
Assim como no trailer, temos duas rodas em e em . Fazendo o momento em temos:
E com isso será pela somatória das forças:
Dessa forma a reação em e serão:
O legal que o mecanismo bota força nas duas rodas, e não cria uma balança, levantando a roda da frente como na questão anterior.