Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 98
98- Resolva o Problema considerando que a carga de foi removida.
Passo 1
Com a força de retirada ficamos com a seguinte distribuição de forças no corpo todo.
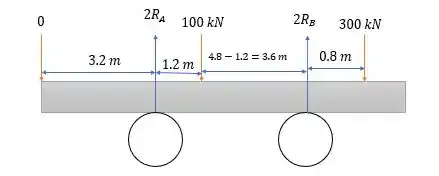
Se aplicarmos o momento em nós iremos ter:
E fazendo a somatória das forças verticais e igualando a zero nós teremos:
Passo 2
Agora analisando o corpo a direita para tirarmos as reações em e .
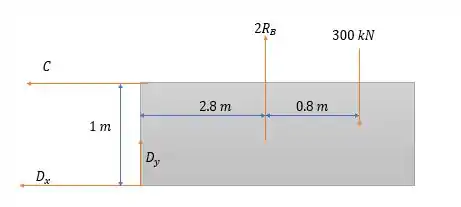
Fazendo a somatória dos momentos em temos:
Logo pela soma das forças horizontais:
E pela soma das forças verticais:
Então a reação em será:
Resposta
Exercícios de Livros Relacionados
7.14. Uma barra semicircular é carregada tal como mostra a figura. Determine a intensidade e a localização do momento fletor máximo na barra.
Sabendo que o raio da roldana é 200m m e desprezando o atrito, determine as forças internas no ponto J da estrutura mostrada na figura.
22. Uma força P é aplicada em uma haste dobrada que é apoiada por um rolete e um suporte com pino. Para cada um dos três casos mostrados, determine as forças internas no ponto J :
23. Uma haste de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 60 ° .
24. Uma haste de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 15 0 ° .