Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 13.Exercícios e Problemas - Ex. 22
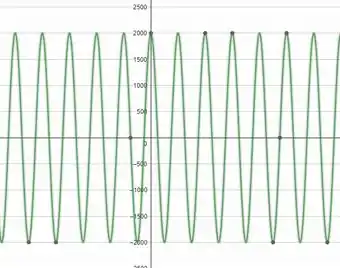
13.22P O conjunto de amortecedores do carro descrito no Problema 13.21 tem uma constante de amortecimento , conforme definição expressa pela Equação 13.59. Suponha que a força vertical sobre o carro provocada pela modulação na estrada tenha o comportamento
Onde é a velocidade de trânsito do carro. Faça um gráfico da amplitude da oscilação vertical do carro em função da sua velocidade.
Passo 1
Belezoca galerinha, temos a função trigonométrica expressa pela equação:
Portanto, com a ajuda de uma ferramenta gráfica, vemos que o gráfico da função é:
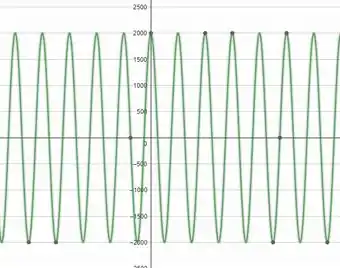
Resposta
Exercícios de Livros Relacionados
O instrumento mostrado possui uma massa de 43 kg e é ligado por molas à base horizontal. Se a amplitude de vibração vertical da base é de 0,10 mm, calcule a faixa de frequências fn de vibração da base
49. Um sistema massa-mola com amortecimento viscoso é excitado por uma força harmônica de amplitude constante F 0 , mas de frequência variável ω . Se a amplitude do movimento em regime permanente decr
47. Uma máquina montada sobre molas, com uma massa de 24k g , vibra harmonicamente na direção vertical, com uma amplitude de 0,30m m , sob a ação de uma força vertical que varia harmonicamente entre F
52. Se a frequência de excitação para o sistema do Problema 8 / 50 é ω = 6r a d / s , determine o valor necessário do coeficiente de amortecimento c se a amplitude em regime permanente não deve excede
50. O carrinho de 30k g é acionado pela força harmônico mostrada na figura. Se c = 0 , determine a faixa das frequências de excitação ω para a qual o módulo da resposta em regime permanece é inferior