Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 139
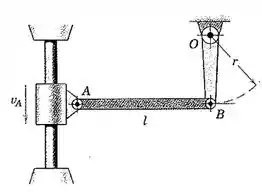
O anel deslizante se desloca para cima e para baixo no eixo, causando uma oscilação da manivela OB. Se a velocidade de A não está variando quando passa a posição zero, onde AB é horizontal e OB é vertical, determine a aceleração angular de OB nessa posição.
Passo 1
Galera, neste exercício nós temos um anel deslizando na vertical com velocidade constante, e queremos saber a aceleração angular provocada em OB.
Vamos olhar o mecanismo.
Neste instante, a velocidade do ponto B é nula, pois não há deslocamento na horizontal. Então, ele é o nosso Centro Instantâneo:
Em relação à OB:
Agora, vamos aplicar a equação de aceleração relativa para a barra AB.
Como
Pela equação: temos enfim:
Resposta
Exercícios de Livros Relacionados
Uma estação de radar B situada no equador observa um satélite A em uma órbita circular equatorial de 200 km de altitude e se movendo de oeste para leste. Para o instante em que o satélite está 30 ° ac
A roda rola sobre a superfície circular sem deslizar. Na posição mais baixa, possui uma velocidade angular ω e uma aceleração angular α , ambas no sentido horário. Para essa posição, obtenha expressõe
A barra de 100N( ≈ 10k g ) está presa com pino a uma estrutura em movimento em A e é mantida em uma posição vertical por uma corda B C que ode suportar uma tração máxima de 50N sem romper a corda. Qua
Uma barra de 900m m repousa em uma mesa horizontal. A força P aplicada como mostrado na figura produz as seguintes acelerações: a A = 3,6m / s 2 para a direita, α = 6r a d / s 2 no sentido anti-horári
No Problema 15.105, determine o ponto da barra que (a) não tem aceleração, (b) tem uma aceleração de 2,4m / s 2 para a direita.