Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 134

Calcule a aceleração angular da placa na posição mostrada, onde a barra de controle AO possui uma velocidade angular constante ω O A = 4 r a d s e   θ = 60 ° para ambas as barras.

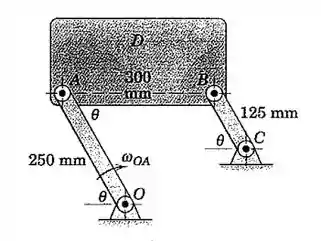
Passo 1

Primeiramente, vamos fazer um esboço do mecanismo com os dados.

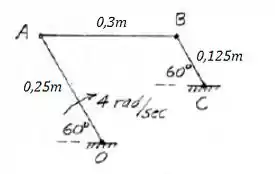
Bom galera, a partir da barra articulada fixa AO, podemos calcular a velocidade e aceleração do ponto A.

v A = ω × r A O = 1   m / s

a A = - ω 2 r A O = - 4 2 0,25 = 4 r a d / s 2

Como a barra BC é movida e neste instante está paralela a AO e os pontos A e B estão na mesma altura, então:

v B = v A = 1   m / s

Analisando agora a barra articulada fixa BC, podemos calcular a aceleração normal do ponto B:

a B n = - ω B C 2 r B C = - v B 2 r B C = 8   m / s 2

Já que não há velocidade relativa de BA, então:

ω A B = 0 → a B / A n = 0

Como Aplicando a equação da aceleração relativa nos pontos A e B:

a B = a A + ( a B / A ) t

Sobrepondo as acelerações encontradas na forma e direção de seus vetores, podemos encontrar a relação dos demais:

Portanto:

a B / A t = a B n - a A c o s 30 ° = 4,62   m / s 2

α = a B / A t A B = 4,62 0,3 = 15,4 r a d s 2 ,   S H

Resposta

α = 15,4 r a d s 2 ,   S H

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 15.238 , considerando que θ = 40 ° .
O braço A B de 5m de comprimento é usado para fornecer uma plataforma elevada para trabalhadores da construção civil. Na posição mostrada na figura, o braço A B está sendo erguido a uma taxa constante
Um disco com raio de 120m m gira à taxa constante ω 2 = 5r a d / s em relação ao braço A B , que, por sua vez, gira à taxa constante ω 1 = 3r a d / s . Para a posição mostrada na figura, determine a v
Sabendo que, no instante mostrado na figura, a barra AB tem uma velocidade angular constante de 6 rad/s no sentido horário, determine a aceleração do ponto D.
No instante mostrado na figura, a barra AB tem uma aceleração angular nula e uma velocidade angular constante de 8 rad/s no sentido horário. Sabendo que l = 0,3 m, determine a aceleração do ponto médi