Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 144

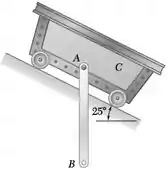
A barra delgada uniforme AB, de massa de 15 kg e comprimento de 1 m, está suspensa como mostra a figura a partir do carrinho C de 20 kg. Desprezando o efeito do atrito, determine, imediatamente depois do sistema ter sido liberado do repouso, (a) a aceleração do carrinho, (b) a aceleração angular da barra.

Passo 1

Cinemática: Resolvemos a aceleração de G na aceleração do carrinho e da aceleração de G em relação a A.

a - R = a G = a A + a G / A

a - R = a C + a G / A

Onde

a G / A = 1 2 L α

Passo 2

Cinética: Carrinho e haste

W R = 15   k g

W C = 20   k g

L = 1   m

I - R = 1 12 m R L 2

a G / A = 1 2 3 α = 1.5 α

+ ↘ Σ F x = Σ F x eff:         W C + W R sin ⁡ 25 ° = m C + m R a C - m R a G / A   cos   25 °

20 + 15 sin ⁡ 25 ° = 1 9,81 20 + 15 a C - 15 1.5 α cos ⁡ 25 °

14,79 = 3,56 a C   - 20,39 α  

a C = ( 14,79 - 20,39 α ) /   3,56  

Passo 3

Haste

+ Σ M A = Σ M A eff:           0 = I - α + m R a G / R L 2 - m R a C cos ⁡ 25 ° L 2

1 12 15 g 3 2 α + 15 g 1.5 α 1.5 - 15 g a C cos ⁡ 25 ° 1.5 = 0

22.5 α + 67.5 α - 45 cos ⁡ 25 ° a C = 0

α = 0.5 cos ⁡ 25 ° a C

Passo 4

  1. Aceleração do carrinho.

    2. Substitua α de (2) para (1):

    a C = 9,81 sin ⁡ 25 ° + 45 10 cos ⁡ 25 ° 0.5 cos ⁡ 25 ° a C

    a C = 9,81 sin ⁡ 25 ° 1 - 22.5 10 cos ⁡ 25 °

    = 3,98   m / s 2

    Passo 2

  2. Aceleração angular.

De (2):

α = 0.5 cos ⁡ 25 ° 18.490

= 8.379   rad/ s 2

Resposta

a C = 3,98   m / s 2     25 °

α = 8.38   rad/ s 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

21. O disco está orginalmente girando a ω 0 = 8 r a d s . Se ele é submetido a uma aceleração angular constante a = 6 r a d s 2 , determine as intensidade da velocidade e das compontes n e t da aceler
No instante mostrado, a roda A gira com uma velocidade angular ω = 6r a d / s e uma aceleração angular α = 3r a d / s 2 . Determine a aceleração angular do segmento BC e a aceleração do pistão C.
A engrenagem rola sobre a cremalheira fixa com uma velocidade angular ω = 12r a d / s e aceleração angular α = 6r a d / s 2 . Determine a aceleração do ponto A .
A engrenagem rola sobre a cremalheira fixa B . No instante mostrado, o centro O da engrenagem se desloca com uma velocidade v O = 6m / s e aceleração a O = 3m / s 2 . Determine a aceleração angular da
Mostre que o par I → α a da chamada da Figura 16.15 pode ser eliminado anexando os vetores , m a - , e m a - n em um Ponto F chamado de centro de percussão, localizado na linha OG a uma distância G P