Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 150

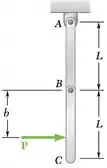
Cada uma das barras AB e BC de 3 kg tem comprimento L = 500 mm. Uma força horizontal P de intensidade de 20 N é aplicada na barra BC. Para a posição mostrada na figura, determine (a) a distância b para a qual as barras se movem como se formassem um único corpo rígido, (b) a correspondente aceleração angular das barras.

Passo 1

O exercício pede que a gente determine a distância b para a qual as barras se movem como se formassem um único corpo rígido, (b) a correspondente aceleração angular das barras.

Consideramos:

Cinemática: Nós escolhemos α = α A B = α B C  

Cinética: Barras AB e BC (atuando como corpo rígido)

m A B C = 2 m

I - = 1 12 2 m 2 L 2

I - = 2 3 m L 2

+ Σ M A = Σ M A eff:           P L + b = I - A B C α + m A B C a B L

P L + b = 2 3 m L 2 α + 2 m L α L

P L + b = 8 3 m L 2 α

Passo 2

Barra BC:

+ Σ M B = Σ M B eff:           P b = I - B C α + m a - B C L 2 = m 12 L 2 α + m 3 2 L α L 2

P b = 5 6 m L 2 α

α = 5 6 P b 5   m L 2

Substituir por α em (1):

P L + b = 8 3 m L 2 6 5 P b m L 2

P l + P b = 16 5 P b

L = 16 5 - 1 b = 11 5 b

b = 5 11 L

Eq. (2)

α = 6 5 P m L 2 5 11 L               α = 6 11 P m L

Passo 3

Dados:

L = 500   mm = 0.5   m

m = 3   kg

P = 20   N

Passo 4

  1. b = 5 11 L = 5 11 0.5 = 0.22727   m

    Passo 5

α = 6 11 P m L = 6 11 20   N 3   kg 0.5   m = 7.2727   rad/ s 2

Resposta

a )   b = 227   mm

b )   α = 7.27   rad/ s 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda desliza enquanto rola. Se v O = 1,2m / s e se a velocidade de A em relação a B é de 0,9 2m / s , localize o centro instantâneo C de velocidade nula e encontra a velocidade do ponto P.
O disco circular gira em torno de seu eixo z com uma velocidade angular ω = 2r a d /s . Um ponto P localizado sobre a borda possui uma velocidade dada por v = - 0,8 i - 0,6 jm / s . Determine as coord
A cuba oscilatória de produtos do Prob. 5/86 é apresentada aqui novamente. Se a manivela OB possui uma velocidade angular constante no sentido anti-horário de 0,944 rad/s, determine a velocidade angul
As duas polias estão presas uma na outra para formar um único conjunto rígido, e cada um dos dois cabos está enrolado firmemente em torno de sua respectiva polia. Se o ponto A no cabo de elevação poss
22. O disco está originalmente girando a ω 0 = 8 r a d s . Se ele é submetido a uma aceleração angular constante a = 6 r a d s 2 , determine as intensidades da velocidade e das compontes n e t da acel