Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 27
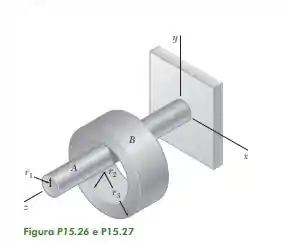
O anel B tem um raio interno e está suspenso por um eixo horizontal A do modo mostrado na figura. O eixo A gira com velocidade angular constante de e não ocorre deslizamento. Sabendo que , e , determine (a) a velocidade angular do anel , (b) a aceleração dos pontos do eixo e do anel que estão em contato, (c) a intensidade da aceleração de um ponto sobre a superfície externa do anel .
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Sabemos que o ponto de contato é em logo:
Na prateleira
Na
A aceleração em é dada por:
Substituindo os valores:
Passo 2
A letra nos pede a aceleração. A aceleração é dada por:
Substituindo os valores
Passo 3
A letra c nos pede a aceleração em ela será, substituindo na fórmula acima:
Resposta
Exercícios de Livros Relacionados
O vetor de velocidade angular de uma bola de futebol que acabou de ser chutada é horizontal e seu eixo de simetria OC é orientado conforme mostrado. Sabendo que a magnitude da velocidade angular é 200
Se a Terra fosse uma esfera, a atração gravitacional do Sol, da Lua e dos planetas seria sempre equivalente a uma única força R agindo no centro de massa da Terra. No entanto, a Terra é na verdade um
Referindo-se ao Problema 18.143, (a) provar que o elipsóide de Poinsot é tangente ao plano invariável, (b) mostrar que o movimento do corpo rígido deve ser tal que o elipsóide de Poinsot pareça rolar
O topo de 85 g mostrado é suportado no Ponto fixo 0. Os raios de giração do topo em relação ao seu eixo de simetria e em relação a um eixo transversal em 0 são 21 mm e 45 mm, respectivamente. Sabendo
O topo mostrado é suportado no Ponto fixo 0 e seus momentos de inércia em torno de seu eixo de simetria e em torno de um eixo transversal em 0 são denotados, respectivamente, por I e I ' . (a) Mostre