Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 79

Se o apoio em B é subitamente removido, determine as componentes vertical e horizontal iniciais da reação que o pino A exerce sobre a barra ACB. Os segmentos AC e CB têm, cada um, uma massa de 5 kg.

Passo 1

Nesse exercício, iremos primeiramente calcular o momento de inércia e as componentes normal e tangencial da aceleração.

Momento de inércia com relação ao centro de massa:

I G = 1 12 m l 2 = 1 12 ( 5 ) ( 0,9 2 )

I G = 0,3375   k g . m 2

Devemos atentar para o fato de que estamos analisando o triângulo composto pela barra AC, até metade da barra CB, com isso, conseguimos encontrar o r G para a barra BC por pitágoras. A visualização se torna mais fácil com o auxílio da seguinte figura:

r G = 0,9 2 + 0,45 2 = 1,0062

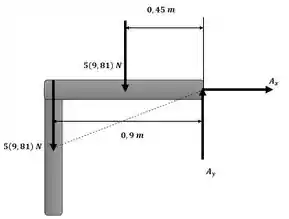
Passo 2

Aproveitando, podemos ainda determinar o ângulo formado entre a barra BC e o vetor logo quando o apoio B é removido, esse ângulo está representado na figura a seguir:

θ = t g - 1 0,45 0,9 → θ = 26,56

Componente normal da aceleração:

a G n A B = a G t B C = ω 2 r G = 0 2 0,9 → a G n = 0   m / s 2

Componente tangencial da aceleração:

a G t A B = α r G = α 0,45

a G t B C = α r G = α 0,9 2 + 0,45 2

a G t B C = 1,0062 α

Agora, podemos aplicar a equação do momento em torno do ponto A:

↺ + ∑ M A = ∑ M k A

5 ( 9,81 ) 0,45 + 5 ( 9,81 ) 0,9 = 0,3375 α + 5 0,45 α 0,45 + 0,3375 α + 5 ( 1,0062 α ) ( 1,0062 )

α = 9,81   r a d / s 2

Passo 3

Agora, podemos aplicar os somatórios de força nas direções x e y para descobrir os valores das reações no ponto A:

Na direção x:

+ → ∑ F x = m a G x

A x = 5 1,0062 9,81 s e n 26,57 °

A x = 22,1   N

Na direção y:

+ ↑ ∑ F y = m a G y

A y - 10 ( 9,81 ) = - 5 0,45 9,81 - 5 1,0062 9,81 c o s 26,57 °

A y = 31,89   N

Resposta

A x = 22,1   N

A y = 31,89   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pequeno motor M é articulado em relação ao eixo x através de O e transmite ao seu eixo AO uma velocidade constante p rad/s no sentido mostrado, em relação á sua carcaça. O conjunto inteiro é, em seg
Uma aeronave não tripulada com radar controlado por rádio e com rotor de propulsão inclinável está sendo projetada para fins de reconhecimento. A elevação vertical iniciada com θ = 0 e é seguida por v
O disco circular maciço de massa m = 2k g e raio r = 100m m rola em circulo de raio b = 200m m sobre o plano horizontal sem deslizar. Se a linha de centro O C do eixo da roda gira em torno do eixo z c
A roda com raio de 100 mm possui uma massa de 3 kg e gira em torno de seu eixo y ' com uma velocidade angular p = 40 ⋅ πr a d / s no sentido indicado. Simultaneamente, o garfo gira em torno do eixo x
A placa retangular, com uma massa de 3 kg e uma pequena espessura uniforme, está soldada no ângulo de 45º ao eixos vertical, que gira com a velocidade angular de 20 ⋅ πr a d / s . Determine a quantida