Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 63

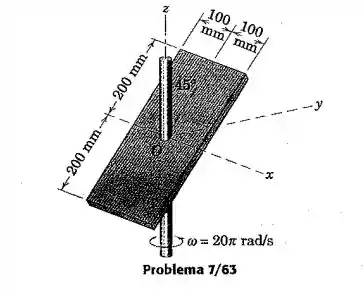
A placa retangular, com uma massa de 3 kg e uma pequena espessura uniforme, está soldada no ângulo de 45º ao eixos vertical, que gira com a velocidade angular de 20 ⋅ π   r a d / s . Determine a quantidade de movimento angular   H → da placa em relação a O e encontre a energia cinética da placa.

Passo 1

Para resolvermos o exercício proposto, vamos precisar estabelecer novos eixos x ' - y ' - z ' convenientes, saindo da origem de forma com que nossa velocidade angular fique mais fácil usar. Usaremos também as relações para H → ' para encontrar H → .

Passo 2

Vamos começar introduzindo esses eixos. Eles estarão posicionados de forma a criar um ângulo de 45º com o eixo inicial, assim teremos que nossas componentes da velocidade angular ω ' → ficaram

ω x ' = 0

ω y ' = 2 2 ⋅ ω  

ω z ' = 2 2 ⋅ ω  

Pois para um ângulo de 45º tanto o seno quanto o cosseno dão o mesmo valor. Agora precisamos calcular o tensor inércia. Como colocamos nosso novo eixo na origem do anterior, nenhuma das dimensões da placa irão mudar, então estamos podemos calcular em relação aos eixos anteriores. Dessa forma, temos que as integrais que serão calculadas são

I x y = ∫ x ⋅ y ⋅ ρ ⋅ d V = 0

I y z = ∫ z ⋅ y ⋅ ρ ⋅ d V = 0

I x z = ∫ x ⋅ z ⋅ ρ ⋅ d V = 0

I y y = ∫ x 2 + z 2 ⋅ ρ ⋅ d V = 1 12 ⋅ m ⋅ 2 ⋅ a 2 = 1 3 ⋅ m ⋅ a 2

I z z = ∫ x 2 + y 2 ⋅ ρ ⋅ d V = 1 12 ⋅ m ⋅ [ 2 ⋅ a 2 + 2 ⋅ b 2 ] = 1 3 ⋅ m ⋅ ( a 2 + b 2 )

Utilizando agora a equação para a quantidade de movimento angular H → ' , temos que

H → ' = I y y ⋅ j → ' - I y z ⋅ k → ' ⋅ 2 2 ⋅ ω

H → ' = 1 3 ⋅ m ⋅ a 2 ⋅ j → ' - 1 3 ⋅ m ⋅ ( a 2 + b 2 ) ⋅ k → ' ⋅ 2 2 ⋅ ω

Mas podemos estabelecer uma relação entre j → ' e k → ' com j ⃗ e k → . Temos que cada um será dado por:

j → ' = j → ⋅ cos ⁡ 45 º + k → ⋅ sin ⁡ 45 º = 2 2 ⋅ j → + k →

k → ' = - j → ⋅ cos ⁡ 45 º + k → ⋅ sin ⁡ 45 º = 2 2 ⋅ - j → + k →

Assim, temos que H → será

H → = 1 6 ⋅ m ⋅ ω ⋅ ( - b 2 ⋅ j → + 2 ⋅ a 2 + b 2 ⋅ k → )

Substituindo os valores para ω , temos que

H → = 1 2 ⋅ 20 ⋅ π ⋅ - 0.04 ⋅ j → + 0.06 ⋅ k → = π ⋅ - 0.4 ⋅ j → + 0.6 ⋅ k →   N ⋅ m ⋅ s

Passo 3

Para a energia T , temos que basta substituirmos na relação T = 1 2 ⋅ ω → ⋅ H →

T = 1 2 ⋅ 20 ⋅ π ⋅ k → r a d s ⋅ π ⋅ - 0.4 ⋅ j → + 0.6 ⋅ k →   N ⋅ m ⋅ s

T = 6 ⋅ π 2 = 59.2   J

Resposta

H → = π ⋅ - 0.4 ⋅ j → + 0.6 ⋅ k →   N ⋅ m ⋅ s

T = 59.2   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco possui uma velocidade angular constante p em torno de seu eixo z , e o garfo A possui uma velocidade angular constante ω 2 em torno de seu eixo, como mostrado. Simultaneamente, o conjunto inte
O cursos e o garfo A recebem uma velocidade ascendente constante de 0,2m / s durante um intervalo de movimento e obrigam a esfera na extremidade da barra a deslizar na ranhura radial no disco em rotaç
Para as condições descritas no Prob. 7/36, determine a velocidade v e a aceleração a do centro A da ferramenta esférica em termos de β .
O rotor do giroscópio mostrado está girando na taxa constante de 100 rpm em relação aos eixos x - y - z , no sentido indicado. Se o ângulo γ entre o anel de suspensão e o plano horizontal X - Y é leva
O eixo esbelto sustenta duas partículas deslocadas cada uma de massa m e gira em relação ao eixo z com uma velocidade angular ω conforme indicado. Escreva uma expressão para a quantidade de movimento