Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 69

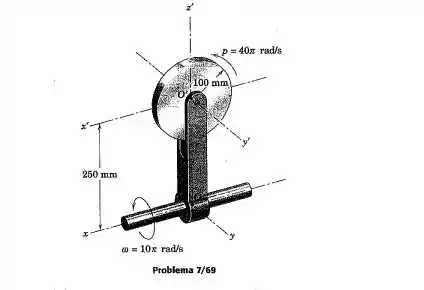
A roda com raio de 100 mm possui uma massa de 3 kg e gira em torno de seu eixo y ' com uma velocidade angular p = 40 ⋅ π   r a d / s no sentido indicado. Simultaneamente, o garfo gira em torno do eixo x de sua haste de suporte com uma velocidade angular ω = 10 ⋅ π   r a d / s conforme indicado. Calcule a quantidade de movimento angular da roda em relação a seu centro O ' . Calcule também a energia cinética da roda.

Passo 1

Vamos utilizar as relações de quantidade de movimento angular para os eixos principais x ' - y ' - z ' e as relações de energia cinética de rotação com os cálculos das componentes dos tensores de inércia.

Passo 2

Temos que x ' - y ' - z ' são os eixos principais de inércia. Assim, temos que nossa quantidade de movimento angular será dada por

H → O ' = I x ' x ' ⋅ i → + I y ' y ' ⋅ j → + I z ' z ' ⋅ k →

Para encontrarmos as componentes do tensor, temos que efetuar o cálculo das seguintes integrais

I x ' x ' = ∫ y 2 + z 2 ⋅ ρ ⋅ d V = 1 4 ⋅ m ⋅ r 2

I y ' y ' = ∫ x 2 + z 2 ⋅ ρ ⋅ d V = 1 2 ⋅ m ⋅ r 2

I z ' z ' = ∫ x 2 + y 2 ⋅ ρ ⋅ d V = 1 4 ⋅ m ⋅ r 2

Temos também que o vetor ω → é dado por ω x = ω , ω y = p e ω z = 0 . Dessa forma, temos substituindo na equação de H o ' → que

H o ' → = 1 4 ⋅ m ⋅ r 2 ⋅ ω ⋅ i → + 1 2 ⋅ m ⋅ r 2 ⋅ p ⋅ j →

H o ' → = 1 4 ⋅ 3   k g ⋅ 0.1   m 2 ⋅ ( 10 ⋅ π   r a d / s ) ⋅ i → + 1 2 ⋅ ( 3   k g ) ⋅ 0.1   m 2 ⋅ ( 40 ⋅ π   r a d / s ) ⋅ j →  

H o ' → = 0.236 ⋅ i → + 8 ⋅ j →   N ⋅ m ⋅ s

Passo 3

Agora para calcular a energia cinética usaremos a relação completa da energia, que é dada por

T = 1 2 ⋅ ω → ⋅ H o ' → + 1 2 ⋅ v → ⋅ G →

T = 1 2 ⋅ ω ⋅ i → + p ⋅ j → ⋅ 1 2 ⋅ m ⋅ r 2 ⋅ ω 2 ⋅ i → + ⋅ p ⋅ j → + 1 2 ⋅ - r ' → ⋅ ω ⋅ j → ⋅ ( - m ⋅ r ' → ⋅ ω ⋅ j → )

Onde r → ' é a distância da origem em x - y - z até a origem x ' - y ' - z ' , ou seja, r ' → = 0.25 ⋅ k → . Assim, temos que nossa energia ficará

T = 1 4 ⋅ m ⋅ r 2 ⋅ 1 2 ⋅ ω 2 + p 2 + 1 2 ⋅ m ⋅ r ' 2 ⋅ ω 2

T = 1 4 ⋅ ( 3   k g ) ⋅ 0.1   m 2 ⋅ 1 2 ⋅ 10 ⋅ π r a d s 2 + 40 ⋅ π r a d s 2 + 1 2 ⋅ 3   k g ⋅ ( 0.25   m ) 2 ⋅ 10 ⋅ π r a d s 2

T = 215   J

Resposta

H o ' → = 0.236 ⋅ i → + 8 ⋅ j →   N ⋅ m ⋅ s

T = 215   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o instante representado, o cursor B está se deslocando ao longo da haste fixa na direção X com uma velocidade constante v B = 4m / s . Também neste instante X = 0,3m e Y = 0,2m . Calcule a veloci
A nave espacial está girando em torno do seu eixo z , que possui uma orientação espacial fixa, na taxa constante p = 1 / 10r a d / s . Simultaneamente, os seus painéis solares estão se desdobrando à t
O centro O da nave espacial está se deslocando através do espaço com uma velocidade constante. Durante o período do movimento anterior à estabilização, a nave espacial possui uma taxa de rotação const
O disco circular com 100 mm de raio gira em torno de seu eixo z com a velocidade constante p = 240r p m , e o braço O C B gira em torno do eixo Y na velocidade constante N = 30r p m . Determine a velo
Para as condições descritas no Exemplo 7/2, exceto que γ está aumentando na taxa constante de 3 ⋅ πr a d / s , determine a velocidade angular ω e a aceleração angular α do rotor quando a posição γ = 3