Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 24

Um arame homogêneo e fino é dobrado na forma do perímetro a seguir. Calcule o seu centro de gravidade.

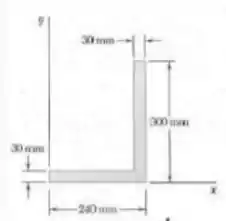
Passo 1

Fala aí galera, vamos pra mais um problema de estática. O primeiro passo é determinar os centroides de cada aresta da figura. Para isso, vamos numerar as arestas da figura no sentido antio-horário. Logo:

x - 1 = 120 × 240 = 28800

x - 2 = 240 × 300 = 72000

x - 3 = 225 × 30 = 6750

x - 4 = 210 × 270 = 56700

x - 5 = 105 × 210 = 22050

x - 6 = 0

y - 1 = 0

y - 2 = 150 × 300 = 45000

y - 3 = 300 × 30 = 9000

y - 4 = 165 × 270 = 44550

y - 5 = 30 × 210 = 6300

y - 6 = 15 × 30 = 450

O perímetro será:

∑ L = 1080 m m

Logo, o centroide será:

x - = 186300 1080 = 172,5 m m

y - = 105300 1080 = 97,5 m m

Resposta

x - = 172,5 m m

y - = 97,5 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y - da área.
Localize o centroide y - da área.
A placa tem uma espessura de 12 mm e é composta de aço com um peso específico de 80 kN/m³. Determine as componentes horizontal e vertical da reação no pino A e a força na corda em B .
Localize o centroide da área. Dica: Escolha elementos de espessura d y e comprimento [ 2 - y - y 2 ] .
Localize o centroide ( x - ,y - ) da área.