Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 235
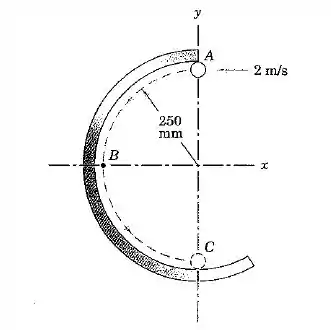
Uma pequena partícula de é projetada com uma velocidade horizontal de no topo da guia circular lisa fixada no plano vertical. Calcule a taxa de variação no tempo da quantidade de movimento angular em torno do ponto quando a partícula passa pela parte inferior da guia em .
Passo 1
Bom galera, nesse exercício queremos encontrar a taxa de variação no tempo da quantidade de movimento angular em torno do ponto . Sabemos que
Passo 2
Substituindo, temos
Isolando , ficamos com
Temos então,
Passo 3
Sabemos pela segunda lei de Newton que
Dessa forma, temos então
Dessa forma, o momento será
Resposta
Exercícios de Livros Relacionados
O cilindro de 50 kg tem uma velocidade angular de 30 rad/s quando é colocado em contato com a superfície horizontal em C. Se o coeficiente de atrito cinético é μ C = 0,2 , determine quanto tempo vai l
O volante de 100 kg tem um raio de giração em relação a seu centro de gravidade O de k O = 0,225m , Se ele gira no sentido anti-horário com uma velocidade angular de 1200 rev/min antes de o freio ser
O volante A de 15 kg tem um raio de giração em relação a seu centro de 100 mm. O disco B tem uma massa de 25 kg e está acoplado ao volante através de uma correia que não desliza em suas superfícies de
O corpo rígido (placa) tem uma massa m e gira com uma velocidade angular ω em relação a um eixo passando pelo ponto fixo O. Demonstre que os momentos de todas as partículas compondo o corpo podem ser
O volante A tem uma massa de 30 kg e um raio de giração k C = 95m m . O disco B tem uma massa de 25 kg, está preso com pino em D, e está acoplado ao volante usando uma correia que está submetida a uma