Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 224
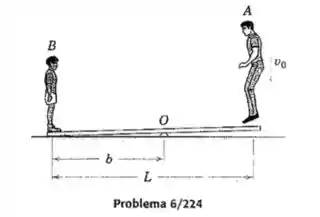
Em uma atração acrobática, um homem de massa pula de uma plataforma elevada sobre a extremidade da viga leve, porem resistente, com uma velocidade . O menino de massa é lançado para cima com uma velocidade . Para uma determinada razão , determine em termos de para maximizar a velocidade do menino para cima. Assuma que tanto o homem quanto o menino se comportam como corpos rígidos.
Passo 1
Bom, vamos considerar dois casos separados, o primeiro é quando o homem salta da plataforma elevada, e está prestes a cair na viga leve, e o segundo, é o momento em q a viga rotaciona e o menino é lançado. Para o primeiro caso, a quantidade de movimento do sistema em relação ao ponto O será:
E para o segundo caso:
Como a variação da quantidade de movimento é zero, podemos fazer:
Passo 2
E como velocidade angular é a mesma para o homem e para o menino no segundo caso:
Podemos então escrever tudo em termos de :
Ficando com:
Isolando :
Como dado no enunciado:
Passo 3
E para encontrarmos a velocidade máxima do menino, precisaremos derivar a velocidade dele em relação ao comprimento b:
Para que o numerador seja zero:
E b será;
O valor negativo foi descartado, pois precisamos de uma velocidade positiva de .
Resolvendo a equação de para esse valor de b nos dá: