Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 32
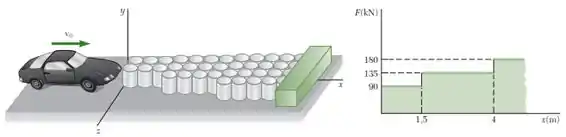
Um automóvel desgovernado deslocando-se a 100 km/h bate de frente com um sistema rodoviário de absorção de impacto (amortecedor) do tipo mostrado na figura, no qual o automóvel é levado ao repouso pelo esmagamento sucessivo de tambores de aço. A intensidade da força necessária para esmagar os tambores é mostrada como uma função da distância de deslocamento do automóvel dentro do amortecedor. Sabendo que a massa do automóvel é 1100 kg e desprezando o efeito do atrito, determine (a) a distância que o automóvel percorrerá dentro do amortecedor antes de atingir o repouso e (b) a desaceleração máxima do automóvel.
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão!
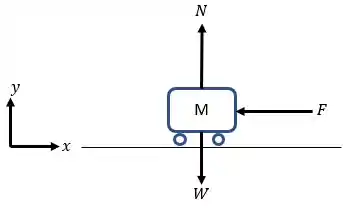
Mas, não é por isto que não devemos identificar as forças do nosso problema e construir um diagrama de corpo livre. Portanto, este é o nosso primeiro passo (e até o mais importante!).
Então, fazendo o diagrama de corpo livre, temos,
Passo 2
Agora, precisamos montar as nossas equações para que possamos resolver a letra a) e a letra b). Para isto, ao observamos o diagrama de corpo livre, percebemos que é apenas a força que realizará trabalho sobre o nosso carro.
Pelo princípio do trabalho e energia, temos que:
Sendo e a energia cinética inicial e final, respectivamente. Elas são expressas por:
E assim chegamos à equação:
Passo 3
Temos agora todas as informações necessárias para resolvermos e letra a). Aqui, queremos determinar a distância que o automóvel percorrerá dentro do amortecedor até o carro parar. Isto é, até a velocidade ser igual a zero! Então, temos:
Temos que descobrir qual a distância necessária para que a força produza o trabalho .
Então, vamos começar analisando por etapas. Nos primeiros , a força é igual a 90 kN. Portanto, o trabalho total realizado pela força nesta região é:
Como , então, o carro não irá parar nesta região! Mas será se o mesmo ocorrerá na região entre 1,5 m e 4 m? Para que isto ocorra, é necessário que o trabalho nesta região seja igual a:
Dada a força , a distância necessária para produzir o trabalho é:
Opa! O carro precisa percorrer uma distância de 2,14 m dentro da segunda região (de forças ). Só que esta região possui um comprimento total de . Logo, o carro conseguirá parar dentro desta região!
Para finalizarmos então a letra a), temos:
Passo 4
E agora chegamos à parte mais fácil da questão! Precisamos determinar a desaceleração máxima do automóvel. Isto é, a intensidade da aceleração.
Pelo nosso diagrama de corpo livre vemos que o carro está submetido apenas a força na direção (a direção em que o carro irá frear). Portanto, temos:
Como a força máxima é , a aceleração máxima será:
E assim finalizamos a letra b).