Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 144
O latão basculante se articula em torno de C e é operado pelo cilindro hidráulico AB. Se o cilindro está estendendo-se a uma taxa constante de 0,15 m/s, determine a velocidade angular do latão no instante em que ele está na posição horizontal mostrada.
Passo 1
Começaremos o exercício analisando o diagrama a seguir:
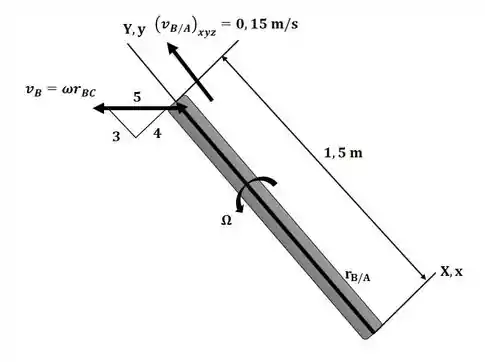
Com base nele, podemos escrever:
E, por sua vez, a velocidade em B:
Passo 2
Agora podemos aplicar a equação da velocidade para os pontos A e B, ainda tomando como base o diagrama do passo 1:
Passo 3
Agora iremos igualar as componentes i e j obtidas no passo 2:
Resposta
Exercícios de Livros Relacionados
Um trenó de foguete é testado em uma pista reta construída ao longo de um meridiano. Sabendo que a pista está localizada na latitude 40 ° norte, determine a aceleração de Coriolis do trenó quando ele
O movimento do bico D é controlado pelo braço AB. No instante mostrado, o braço está girando no sentido anti-horário a uma taxa constante w = 2,4 rad / s e a porção BC está sendo estendida a uma taxa
Resolva o Problema 15.221, supondo que no instante mostrado a velocidade angular ω 1 da haste é 3 rad / s e está aumentando a uma taxa de 12 rad / s², enquanto a velocidade relativa u do colar é 34 in
O guindaste mostrado gira a uma taxa constante col = 0,25 rad / s; simultaneamente, a lança telescópica está sendo abaixada a uma taxa constante ω 2 = 0.40 r a d / s . Sabendo que, no instante mostrad
Na posição mostrada, a haste fina se move a uma velocidade constante u = 3 in./s para fora do tubo BC. Ao mesmo tempo, o tubo BC gira a uma taxa constante ω 2 = 1.5 r a d / s em relação ao braço CD. S