Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 87

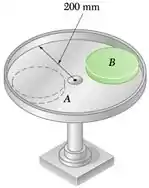
Uma plataforma circular A é presa a um aro de raio interno de 200 mm e pode girar livremente sobre um eixo vertical. É sabido que a unidade plataforma-aro tem massa de 5 kg e raio de giração de 175 mm com relação ao eixo. No momento em que a plataforma está girando com uma velocidade de 50 rpm, um disco B de 3 kg e raio de 80 mm é colocado na plataforma com velocidade nula. Sabendo que o disco B, então, desliza de encontro ao aro até ficar em repouso relativo à plataforma, determine a velocidade angular final da plataforma.

Passo 1

O enunciado pede que a gente, determine a velocidade angular final da plataforma.

Momentos de inércia.

I - A = m A k 2 = 5   kg 0.175   m 2 = 0.153125   kg ∙ m 2

I - B = 1 2 m B r B 2 = 1 2 3   kg 0.08   m 2 = 9.6 × 10 - 3  kg ∙ m 2

Passo 2

Estado 1. O disco B está em repouso.

Estado 2. O disco B se move com a plataforma A.

Cinemática.

No Estado 2,

v - B = 0.12   m ω 2

Passo 3

Princípio de conservação do momento angular.

+ Momentos sobre D:

I - A ω 1 = I - A ω 2 + I - B ω 2 + m B v - B 0.12   m

0.153425   kg ∙ m 2 ω 1 = 0.153425   kg ∙ m 2 ω 2

+ 9.6 × 10 - 3   kg ∙ m 2 ω 2 + 3   kg 0.12   m 2 ω 2

0.153125 ω 2 = 0.20593 ω 1

ω 2 = 0.7436 ω 1 = 0.7436 50   rpm

Resposta

Velocidade angular final

ω 2 = 37.2   rpm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O volante de 350 kg de um pequeno guincho tem um raio de giração de 600 mm. Se o motor é desligado quando a velocidade angular do volante é de 100 rpm no sentido horário, determine o tempo necessário
Mostre que, quando uma placa rígida gira em torno de um eixo fixo através de 0 perpendicular à placa, o sistema de momentos de suas partículas é equivalente a um único vetor de magnitude m r - ω , per
Um cilindro de 3 kg de raio r 125 mm com uma velocidade angular inicial 0 90 rad /s no sentido anti-horário é colocado no canto formado pelo piso e por uma parede vertical. Sabendo que o coeficiente d
Um cilindro de raio r e peso W com velocidade angular inicial 0 no sentido anti-horário é colocado no canto formado pelo piso e por uma parede vertical. Representando por k o coeficiente de atrito cin
O disco B também tem uma velocidade angular inicial quando é colocado em contato com o disco A que está em repouso. Mostre que a velocidade angular final do disco B depende apenas de ω 0 e da razão da