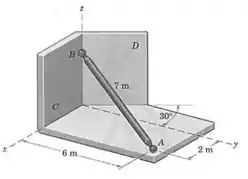
Uma das paredes verticais que apoiam a extremidade do eixo uniforme de do exemplo é girada de um ângulo de , como mostrado aqui. A extremidade permanece ainda apoiada por uma rótula no plano horizontal -. Calcule os módulos das forças e exercidas na extremidade esférica do eixo pelas paredes verticais e , respectivamente.

Para que o eixo esteja em equilíbrio é preciso que os momentos e as forças resultantes seja nulos. Vamos escrever uma equação de equilíbrio que facilite a nossa conta.

Se calcularmos o momento em relação ao ponto , por exemplo, a força (que é desconhecida) vai sumir da equação, e só vão sobrar as forças , e :

Onde os vetores são as posições do ponto de atuação de cada força em relação ao ponto . Como as forças e atuam no mesmo ponto:

E precisamos escrever cada um desses vetores:

Onde é a seguinte altura:

Que a gente pode calcular usando o teorema de pitágoras:

Então:

E o outro vetor é o que liga o ponto ao centro de massa do eixo:

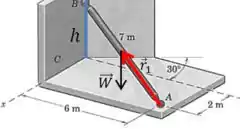
Como o centro de massa está exatamente na metade do eixo:

E agora já temos tudo para resolver os produtos vetoriais.

Vamos voltar na nossa equação de equilíbrio:

Primeiro vamos resolver a soma de vetores que está entre parênteses:

E agora vamos substituir tudo na equação principal:

Cada um desses produtos vetoriais pode ser escrito como o determinante de uma matriz, então:

E agora queremos que cada componente se anule, então:

Agora podemos resolver esse sistema para encontrar as duas variáveis. Pela segunda equação temos:

E substituindo isso na primeira equação:

Resolvido! Nem precisamos usar a terceira equação!