Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 23

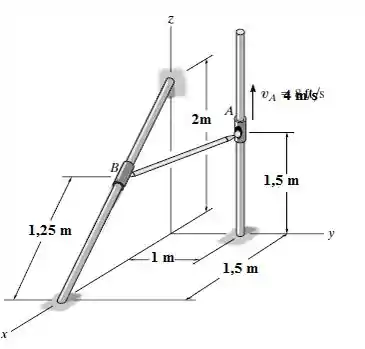
A barra AB está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A tem uma velocidade Va = 4k m/s, determine a velocidade angular da barra e a velocidade do anel B nesse instante. Suponha que a velocidade angular da barra é direcionada perpendicular à barra

Passo 1

Definir vetores:

r a / b =     0,75 i     -   1 j   –   0,5 k

V b   = - 3 / 5 V b   i   +   4 / 5 V b   k

V a   =   4   K

ω   =   ω x   i   + ω y     j   +   ω z   k

Passo 2

Encontrando a velocidade no ponto B.

V b   =   V a   + ω   x   r a / b

Substituindo:

- 3 / 5   V b i   + 4 / 5   V b   k = 4   K + ( ω x   i   + ω y     j   +   ω z   k   )   x   ( 0,75 i     -   1 j   –   0,5 k )

Passo 3

Separando os valores por componentes i,j e k. Teremos:

- 3 / 5 V b =   ω z   -   0,5   ω y

4 / 5 V b   =   0,5 ω x +   0,75 ω z  

4   =   ω x + 0,75 ω y

Por haver 3 equações e 4 incógnitas faz-se necessário encontrar uma 4° equação.

ω .   r a / b   = 0

( ω x   i   + ω y     j   +   ω z   k ).( 0,75i - 1j - 0,5k) = o

0,75 ω x - ω y – 0,5 ω z = 0

Organizando as equações temos:

ω z   -   0,5   ω y + 3 / 5 V b = 0

  0,5 ω x +   0,75 ω z - 4 / 5 V b   = 0  

  ω x + 0,75 ω y - 4 = 0

0,75 ω x - ω y – 0,5 ω z = 0

Aplicando eliminação de Gauss poderemos obter os resultados, sugere-se a utilização de algum software ou aplicativo para a resolução do sistema, pois se torna uma matriz 4x4 tornado inviável a resolução manual:

V b = 2,35   m / s , ω   =   1,71   i   + 1,27     j -   0,779   k

Resposta

Assim a velocidade em B é =2,35 m/s, e as velocidades angulares são:   ω x = 1,17 rad/s, ω y = 1,27 rad/s e ω z = - 0,779 rad/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra AB está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A tem uma velocidade Va = 1,5 m/s, determine a velocidade angular da barra e a velocidade do anel B mo instante m
A barra AB está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A tem uma aceleração a A=4 im / s ² ² e uma velocidade V a = 1,5im / s , determine a aceleração angular da barra
52. Se a cunha se desloca para a esquerda com uma velocidade constante v , determine a velocidade angular da barra como uma função de θ .
O anemômetro localizado no barco A gira em torno de seu próprio eixo a uma taxa w s , enquanto o barco rola em torno do eixo x com taxa de w x e em torno do eixo y com taxa de w y . Determine a veloci
O movimento do topo e tal que, no instante mostrado, ele gira em torno do eixo z a ω 1 = 0,6r a d / s , enquanto ele rodopia a ω 2 = 8r a d / s . Determine a velocidade angular e aceleração angular do