Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 44

O carrinho de mão tem uma massa de 200 kg e centro de massa em G. Determine as reações normais em cada uma das duas rodas em A e em B se uma força de P = 50 N for aplicada à alça. Despreze a massa das rodas.

Passo 1

Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².

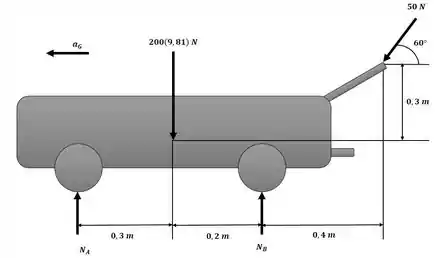
Iniciaremos o exercício aplicando as equações de movimento ao sistema ilustrado na figura a seguir, e lembrando que queremos a reação em cada uma das rodas, ou seja, 2 rodas em A e mais duas em B.

Passo 2

Aplicando as equações de movimento, temos, primeiramente, o somatório de momentos em torno do centro de massa:

↺ + ∑ M G = 0

- 2 N A 0,3 + 2 N B 0,2 + 50 c o s 60 ° 0,3 - 50 sen ⁡ 60 ° 0,6 = 0

Agora, o somatório de forças em na direção x:

+ → ∑ F x = m a G x

50 c o s 60 ° = 200 a G

a G = 0,125   m / s 2

E, por fim, o somatório de forças na direção y:

+ ↑ ∑ F y = m a G y

2 N A + 2 N B - 200 9,81 - 50 s e n 60 ° = 0

Passo 3

Agora, iremos resolver o sistema de duas equações que restou, isolando N A da última equação do passo 2 e substituindo na primeira, temos:

- 2 N A 0,3 + 2 N B 0,2 + 50 c o s 60 ° 0,3 - 50 sen ⁡ 60 ° 0,6 = 0

- 2 ( 2005,3 - N B ) 0,3 + 2 N B 0,2 + 50 c o s 60 ° 0,3 - 50 sen ⁡ 60 ° 0,6 = 0

E, resolvendo para N B , obtemos:

N B = 620   N

Substituindo novamente na última equação do passo 2, podemos encontrar N A :

2 N A + 2 N B - 200 9,81 - 50 s e n 60 ° = 0

2 N A + 2 ( 620 ) - 200 9,81 - 50 s e n 60 ° = 0

N A = 382,6   N

Resposta

N A = 382,6   N

N B = 620   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco de 50 kg está submetido ao momento de binário M = (9t) N.m, onde t é dado em segundos. Determine a velocidade angular do disco quando t = 4 s partindo do repouso.
No instante mostrado, a barra fina uniforme de 30 kg tem uma velocidade angular no sentido horário de ω = 6r a d / s . Determine as componentes normais e tangenciais da reação do pino O sobre a barra
A barra uniforme tem uma massa de 15 kg. Determine as componentes verticais e horizontais da reação no pino O, e a aceleração angular da barra logo após a barra ser cortada.
O hemisfério é formado girando-se a área sombreada em torno do eixo y . Determine o mometo de inércia I y e expresse o resultado em termos da massa total m do hemisfério. O material tem uma densidade
Determine o momento de inércia I y para a barra fina. A densidade da barra ρ e a área de seção transversal A são constante. Expresse o resultado em termos da massa total m da barra.