Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 83

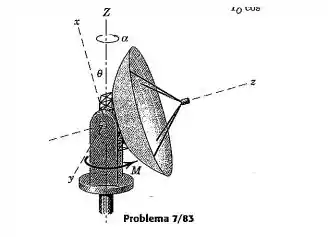
A grande antena para rastreamento de satélite possui um momento de inércia I em relação a seu eixo z de simetria e um momento de inércia I o em relação a cada um dos eixos x e y . Determine a aceleração angular α da antena em relação ao eixo vertical Z , provocada por um torque M aplicado em torno de Z pelo mecanismo de acionamento, para uma determinada orientação θ .

Passo 1

Para resolvermos esse problema vamos usar as relações da Eq. 3/10 e também as de momento fletor para o torque aplicado na antena.

Passo 2

Temos que o torque é aplicado em torno do eixo z , assim temos a seguinte relação

∑ M Z = M = I Z ⋅ α

Vamos ter então que α = M I Z e precisamos calcular o momento de inércia do satélite. Pela relação 3/10 do livro, temos que I Z é dado por

I Z = I x x ⋅ l 2 + I y y ⋅ m 2 + I z z ⋅ n 2

Onde l = cos ⁡ θ ,   m = 0   e   n = sin ⁡ θ . Assim temos que

I Z = I x x ⋅ cos ⁡ θ 2 + 0 + I z z ⋅ sin ⁡ θ 2

Mas nos é dado no exercício que I x x = I O   e   I z z = I . Substituindo então, temos que

I Z = I O ⋅ cos ⁡ θ 2 + 0 + I ⋅ sin ⁡ θ 2

Voltando para a relação do momento fletor, ficamos com

α = M I O ⋅ cos ⁡ θ 2 + 0 + I ⋅ sin ⁡ θ 2  

Resposta

α = M I O ⋅ cos ⁡ θ 2 + 0 + I ⋅ sin ⁡ θ 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o motor gira em torno do eixo x na taxa constante γ ˙ = 3 π r a d / s , sem rotação em torno do eixo Z, determine a aceleração angular do rotor e do disco no instante em que a posição γ = 30 ° é cr
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . O conjunto inteiro gira em torno do eixo vertical Z na taxa
Se o motor atinge uma velocidade de 3000 rpm em dois segundos a partir do repouso com aceleração constante, determine a aceleração angular total do rotor e do disco 1/3 de segundo após ser ligado, se
O ventilador de 4 pás gira em torno do eixo fixo OB com uma velocidade angular constante de N = 1200 rpm. Escreva as expressões vetoriais para a velocidade v e a aceleração a da extremidade A da pá do
O disco circular está girando em torno do eixo OC com velocidade angular constante ω =20r a d / s . Em um determinado instante, o ponto A sobre a borda passa por um ponto cujas coordenadas x-y-z são 4