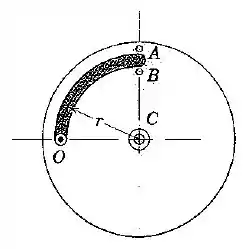
A barra curva de massa é articulada ao disco que gira em e se apoia contra um dos pinos liso e que estão fixados no disco. Se o disco gira em torno de seu eixo vertical , determine a força exercida na barra pela articulação em e a reação ou sobre a barra (a) se o disco possui uma velocidade angular cosntante e (b) quando o disco parte do repouso com uma aceleração angular no sentido anti-horário .
Passo 1
(a) Vamos começar considerando o caso em que a velocidade angular é constante e, portanto, a única aceleração que age sobre a barra curva é centrípeta:
E então a aceleração do centro de massa será:
Onde é a posição do centro de massa da barra curva, um valor que pode ser verificado em alguma tabela:
E a distância entre o centro de massa e o ponto pode ser calculada com um pouco de trigonometria:

Então:
E a única força que produz momento em relação ao ponto é a força de contato em , que deve apontar na direção centrípeta:
Portanto:
Como a única aceleração que age sobre a barra é a resultante centrípeta (que deve ser a mesma para todos os pontos da barra), então podemos deduzir que a força no ponto é a mesma, e só terá uma componente vertical:
Passo 2
(b) Agora vamos analisar o caso em que o disco parte do repouso com uma aceleração angular no sentido anti-horário.
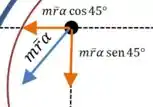
Aplicando a segunda lei de Newton em cada direção:
E na direção vertical:
Passo 3
E para calcular podemos considerar a soma dos momentos em relação ao ponto , no caso em que o disco se move com aceleração angular :
E única força que possui momento em relação a esse ponto é a componente vertical da força em :
Então:
E com isso podemos calcular também o módulo da força em :
Resposta
(a) .
(b) e