Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 116

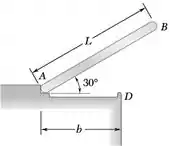
Um barra delgada de comprimento L e massa m é liberada do repouso na posição mostrada na figura e atinge a borda D. Considerando que o impacto em D é perfeitamente plástico, determine, para b = 0,6L, (a) a velocidade angular da barra imediatamente após o impacto, (b) o máximo ângulo que a barra irá girar após o impacto.

Passo 1

Para a análise do movimento de queda antes do impacto, use o princípio de conservação de energia.

Posição 1:

T 1 = 0             V 1 = m g L 4

Posição 2:

V 2 = 0

T 2 = 1 2 m 1 2 ω 2 2 + 1 2 1 12 m L 2 ω 2 2

T 2 = 1 6 m L 2 ω 2 2

T 1 + V 1 = T 2 + V 2 :               0 + m g L 4 = 1 6 m L 2 ω 2 2                 ω 2 = 3 g 2 L

Passo 2

Análise do impacto. Cinemática.

Antes do impacto, a rotação é sobre o Ponto A.

v - 2 = L 2 ω 2

Depois do impacto, a rotação é sobre o Ponto D.

v - 3 = L 10 ω 3

Passo 3

+ Momentos sobre D:

I - ω 2 - m v - 2 L 10 = I - ω 3 + m v - 3 L 10

1 12 m L 2 ω 2 - m L 2 ω 2 L 10 = 1 12 m L 2 ω 3 + m L 10 ω 3 L 10

1 12 - 1 20 ω 2 = 1 12 - 1 100 ω 3

Passo 4

  1. Velocidade angular.

    2. ω 3 = 5 14 ω 2 = 5 14 3 g 2 L

    Para análise da rotação em torno do Ponto D após o impacto use o princípio de conservação de energia.

    Position 3 (Logo após o impacto)

    v - 3 = L 10 ω 3               V 3 = 0

    T 3 = 1 2 m l 10 ω 3 2 + 1 2 1 12 m L 2 ω 3 2 = 14 300 m L 2 ω 3 2 = 14 300 m L 2 5 14 2 g 2 L 2 = m g L 112

    Passo 5

    Posição 4.

    θ = Ângulo máximo de rotação .

    h ' = L 10 sin ⁡ θ

    V 4 = m g h ' = m g l 10 sin ⁡ θ

    v - 4 = 0 ,               ω 4 = 0 ,               T 4 = 0

    T 3 + V 3 = T 4 + V 4 ;               m g l 112 + 0 = 0 + m g l 10 sin ⁡ θ

    Passo 6

  2. Ângulo máximo de rotação.

sin ⁡ θ = 10 112

Resposta

a )   ω 3 = 0.437 g L

b )   θ = 5.12 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A esfera de 6k g e o bloco de 4k g (mostrado em corte) estão presos ao braço de massa desprezível que gira no plano vertical em torno de um eixo horizontal em O . O tampão de 2k g é liberado a partir
A força central de atração F sobre um satélite da Terra não pode ter nenhum momento em tordo do centro O da Terra. Para a órbita elíptica específica com eixos maior e menor conforme indicado, um satél
Determine o módulo H 0 da quantidade de movimento angular da esfera de 2k g em torno do ponto O ( a ) usando a definição vetorial da quantidade de movimento angular e ( b ) usando uma abordagem escala
Uma partícula de massa m se desloca com atrito desprezível sobre uma superfície horizontal e está conectada a uma mola leve presa em O . Na posição A a partícula tem a velocidade v A = 4m / s . Determ
A partícula de massa m é suavemente empurrada a partir da posição de equilíbrio A e posteriormente desliza ao longo da trajetória circular lisa que se situa num plano vertical. Determine o módulo da s