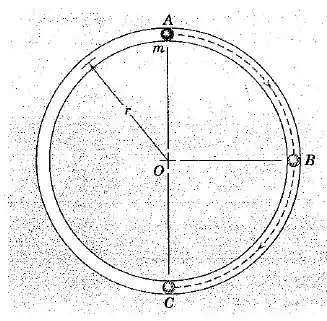
A partícula de massa é suavemente empurrada a partir da posição de equilíbrio e posteriormente desliza ao longo da trajetória circular lisa que se situa num plano vertical. Determine o módulo da sua quantidade de movimento angular em torno do ponto quando ela passa o ponto e o ponto C. Em cada caso, determine a taxa de variação no tempo .
Passo 1
Bom galera, nesse exercício queremos encontrar o módulo da quantidade de movimento angular em torno do ponto .
Sabemos que por definição, a velocidade no ponto é
Passo 2
Substituindo na definição de , temos
Sua taxa de variação ao longo do tempo então será
Passo 3
Para o ponto , temos que
Substituindo na definição da quantidade de movimento angular, temos
Dessa forma, sua taxa de variação temporal será