Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 146

Uma barra delgada AB de 5 kg é conectada por pino em um disco uniforme de 8 kg como mostrado na figura. Imediatamente após o sistema ser liberado do repouso, determine a aceleração do (a) ponto A, (b) ponto B.

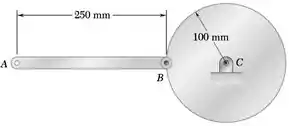
Passo 1

O exercício pede que a gente determine aceleração do (a) ponto A, (b) ponto B. Então consideramos:

Cinemática:

ω = 0

a B = r α C ↓

+ ↓ a - = a B + a G / B

a - = r α C + L 2 α A B ↓

Passo 2

Cinética: Disco

+ Σ M C = Σ M C eff:           B r = I - α C

B r = 1 2 m C r 2 α C

B = 1 2 m C r α C

Passo 3

Barra AB:

+ Σ M G = Σ M G eff:           B L 2 = I - α A B

1 2 m C r α C L 2 = 1 12 m A B L 2 α A B

α C = 1 3 m A B m C ∙ L r α A B

+ ↓ Σ F y = Σ F y eff:           m A B - B = m A B a -

m A B g - 1 2 m C r α C = m A B r α C + L 2 α A B

g = L 2 α A B + 1 2 m C m A B + 1 r α C

g L = 1 2 α A B + 1 2 m C m A B + 1 r L ∙ 1 3 m A B m C ∙ L r α A B

g L = 1 2 + 1 6 + 1 3 m A B m C α A B = 1 3 2 + m A B m C α A B

α A B = 3 g L 1 2 + m A B m C

Passo 4

Dados:

m A B = 5   kg ,             m C = 8   kg ,             r = 0.1   m ,             L = 0.25   m

Eq. (1):

α A B = 3 9.81 m/ s 2 0.25   m ∙ 1 2 + 5   kg 8   kg = 44.846   rad/ s 2  

Eq. (2):

α C = 1 3 5   kg 8   kg ∙ 0.25   m 0.1   m ∙ 44.846   rad/ s 2 = 23.357   rad/ s 2  

Passo 5

b) Aceleração de B.

a B = r α C

= 0.1   m 23.357   rad/ s 2

= 2.336   m/ s 2

Passo 6

a) Aceleração de A.

+ ↓ a A = a B + a B / A

a A = a B + L α A B ↓

a A = 2.336   m/ s 2

+ 0.25   m 44.846   rad/ s 2

a A = 2.336 + 11.212

Resposta

a B = 2.34   m/ s 2 ↓

a A = 13.55   m/ s 2 ↓

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que no instante mostrado na figura a velocidade angular da barra BE é de 4r a d/ s no sentido anti-horário, determine (a) a velocidade angular da barra AD, (b) a velocidade do colar D, (c) a v
Sabendo que no instante mostrado na figura a velocidade do colar D é de 1,6m / s para cima, determine (a) a velocidade angular da barra AD, (b) a velocidade do ponto B, (c) a velocidade do ponto A.
A barra AB desliza livremente ao longo do chão e no plano inclinado. Deduza por v A a velocidade do ponto A , obtenha uma expressão para (a) velocidade angular da barra, (b) a velocidade da extremidad
A barra AB desliza livremente ao longo do chão e no plano inclinado. Sabendo que θ = 20 ° , β = 50 ° , l = 0,6m , v A = 3m / s , determine (a) velocidade angular da barra, (b) a velocidade da extremid
O braço ABD está conectado por pinos ao colar em B e à manivela DE. Sabendo que a velocidade do colar B é de 400m m / s para cima, determine (a) a velocidade angular do braço ABD e (b) a velocidade do