Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 88

A barra AB desliza livremente ao longo do chão e no plano inclinado. Deduza por v A a velocidade do ponto A , obtenha uma expressão para (a) velocidade angular da barra, (b) a velocidade da extremidade B .

Passo 1

A moda agora é a questão 88!

Bom! Pra começar, vamos fazer um esboço da barra, representando vetorialmente as velocidades e o centro de rotação...

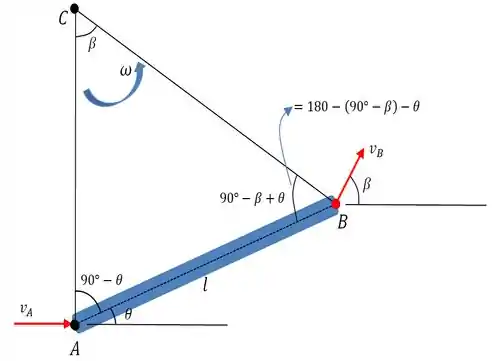
Passo 2

a) Bom! Inicialmente, a gente quer a velocidade angular da barra!

Pois muito bem! O único dado que a gente tem é a velocidade v A e o comprimento l da barra...

C   é o centro de rotação! Pela figura, temos então, a seguinte fórmula...

v A = A C ω

Passo 3

E como determinar A C , dado que só temos l ?

Ora bolas! Molezinha! É só recorrer à lei dos senos...

A C sen ⁡ 90 ° - β + θ = B C sen ⁡ 90 ° - θ = A B sen ⁡ β

A C sen ⁡ [ 90 ° - ( β - θ ) ] = B C sen ⁡ 90 ° - θ = l sen ⁡ β

Mas podemos fazer algumas alterações aí! Se liga na fórmula do seno da diferença abaixo...

sen ⁡ ( a - b ) = sen ⁡ a cos ⁡ b - sen ⁡ b cos ⁡ a

Baseado nisso, podemos reescrever sen ⁡ [ 90 ° - ( β - θ ) ] como...

sen ⁡ [ 90 ° - ( β - θ ) ] = sen ⁡ 90 ° cos ⁡ ( β - θ ) - sen ⁡ ( β - θ ) cos ⁡ 90 °

sen ⁡ [ 90 ° - ( β - θ ) ] = cos ⁡ ( β - θ )

E sen ⁡ 90 ° - θ , obviamente pode ser reescrito como...

sen ⁡ 90 ° - θ = cos ⁡ θ

Chegamos então, à seguinte relação...

A C cos ⁡ ( β - θ ) = B C cos ⁡ θ = l sen ⁡ β

Passo 4

A C então, vai ser dado por...

A C cos ⁡ ( β - θ ) = B C cos ⁡ θ = l sen ⁡ β

A C = l cos ⁡ ( β - θ ) sen ⁡ β

E B C , por sua vez...

B C cos ⁡ θ = l sen ⁡ β

B C = l cos ⁡ θ sen ⁡ β

Passo 5

Pronto! Agora, vamos voltar à formula do P a s s o   2 ...

v A = A C ω

v A = ω l cos ⁡ ( β - θ ) sen ⁡ β

Isolando ω , podemos obter a velocidade angular...

ω = v A l ⋅ sen ⁡ β cos ⁡ ( β - θ )

Passo 6

b) Finalmente, uma vez obtida ω , para encontrar a velocidade em B , basta usar a fórmula abaixo...

v B = B C ω

Onde B C é a distância entre B e o centro de rotação em C !

Substituindo o valor de ω e B C , obtidos anteriormente:

v B = B C ω

v B = l cos ⁡ θ sen ⁡ β v A l ⋅ sen ⁡ β cos ⁡ β - θ

v B = v A cos ⁡ θ cos ⁡ β - θ

Conseguimos obter v B em função de v A !

Feshow!? Hasta la vista guys!

Resposta

a)

ω = v A l ⋅ sen ⁡ β cos ⁡ ( β - θ )

b)

v B = v A cos ⁡ θ cos ⁡ β - θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9. Determine a velocidade angular da bobina. O cabo se enrola em torno do núcleo interno e a bobina não desliza na plataforma P.
7. Se o rolete A se desloca para a direita com uma velocidade constante v A = 3m / s , determine a velocidade angular da barra de ligação e a velocidade do rolete B no instante θ = 30 ° .
34. Se o eixo e a placa giram com uma velocidade angular constante ω = 14 r a d s , determine a velocidade e aceleração no ponto C localizado no canto da placa no instante mostrado. Expresse o resulta
40. O disco A rola sem deslizar sobre a superfície do cilindro fixo B. Determine a velocidade angular de A se seu centro C tem uma velocidade v C = 5 m s . Quantas revoluções A realizará em torno de s
33. Se a barra parte do repouso na posição mostrada e um motor a aciona por um curto período com uma aceleração angular a = 1,5 e t r a d s 2 , onde t é dado em segundos, determine a intensidade da ve