Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas fundamentais - Ex. 21

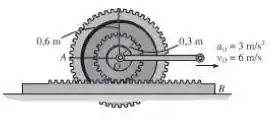
A engrenagem rola sobre a cremalheira fixa B . No instante mostrado, o centro O da engrenagem se desloca com uma velocidade v O = 6   m / s e aceleração a O = 3   m / s 2 . Determine a aceleração angular da engrenagem e a aceleração do ponto A nesse instante.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O exercício nos pede a aceleração angular, α , e a aceleração do ponto A , a A .

Para a aceleração do ponto A , temos a seguinte equação:

a A = a O + α × r A / O - ω 2 r A / O

Observando a equação acima, é possível notar que precisaremos saber o valor da aceleração angular da engrenagem ω .

Sabemos que:

ω = v O r O

Portanto:

ω = 6 0 , 3

ω = 2 0   r a d / s

Vamos descobrir quem é α , analisando primeiro, o movimento relativo de O para B .

a O = a B + α × r O / B - ω 2 r O / B

Temos que, as direções vetoriais dos fatores acima são:

a O = 3 i

a B = a B j

α = - α k

r O / B = 0,3 j

Logo:

3 i = a B j + ( - α k ) × 0,3 j - 20 2 0,3 j

O produto vetorial:

- k × j = i

Portanto:

3 i = a B j + 0,3 α i - 120 j

Organizando cada vetor, temos:

3 i = 0,3 α i

0 = a B j - 120 j

Temos que:

0 , 3 α = 3

α = 10   r a d / s 2

E:

a B = 120   m / s 2

Passo 2

Agora que descobrimos α , podemos resolvero o nosso problema:

a A = a O + α × r A / O - ω 2 r A / O

a O = 3 i

α = - 10 k

r A / O = - 0 , 6 i

a A = 3 i + ( - 10 k ) × - 0 , 6 i - 20 2 - 0,6 i

O produto vetorial:

- k × - i = j

Portanto:

a A = 3 i + 6 j + 240 i

a A = 243 i + 6 j   m / s 2

Resposta

a A = 243 i + 6 j   m / s 2

α = 10   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga AE de 2,5m está sendo baixada por dois guindastes. No instante mostrado na figura, sabe-se que a velocidade do ponto D é de 600m m / s para baixo e que a velocidade do ponto E é de 900m m / s p
Um helicóptero desloca-se horizontalmente na direção x a uma velocidade de 200k m / h . Sabendo que as lâminas principais giram no sentido horário com uma velocidade angular de 180r p m , determine o
O carretel de fita e sua estrutura de apoio são puxados para cima com uma velocidade v A = 750m m / s . Sabendo que o carretel de 80 mm de raio tem uma velocidade angular de 15r a d / s no sentido hor
O carretel de fita e sua estrutura de apoio são puxados para cima com uma velocidade v A = 100m m / s . Sabendo que a extremidade B da fita é puxada para baixo com velocidade de 300m m / s e que, no i
Resolva o Problema Resolvido 15.2, considerando que a cremalheira inferior não é fixa, mas se desloca para a esquerda com velocidade de 0,6m / s .