Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 145

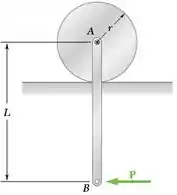
Uma barra delgada uniforme AB de massa m está suspensa como mostra a figura a partir de um disco uniforme de mesma massa m. Determine as acelerações nos pontos A e B imediatamente após a força horizontal P ter sido aplicada em B.

Passo 1

O exercício pede que a gente determine as acelerações nos pontos A e B imediatamente após a força horizontal P ter sido aplicada em B.

Cinemática:

ω = 0

Rolando sem deslizar

a C x = 0

→ + a A = a C x + a A / C = 0 + r α A

a A = r α A →

Haste AB:

α A = a A r

→ + a A = L 2 α A B - a - A B

Passo 2

Cinética:

+ Σ M C = Σ M C eff:           A x r = m a A r + I - α A

Cilindro:

A x r = m a A r + 1 2 m r 2 a A r

A x = 3 2 m a A

A x = 3 2 m L 2 α A B - a - A B

Passo 3

Haste AB:

+ Σ M A = Σ M A eff:           P L = m a - A B L 2 + I - α A B

P L = m a - A B L 2 + m 12 L 2 α A B

← + Σ F x = Σ F x eff:           P + A x = m a - A B

Substituir de (1)

P + 3 2 m L 2 α A B - a - A B = m a - A B

P = 5 2 m a - A B - 3 4 m L 2 α A B

Multiplicando por L 9 :

1 9 P L = 5 L 18 m a - A B - 1 12 m L 2 α A B

(4) + (2):

10 9 P L = 1 2 + 5 18 m L a - A B = 7 9 m L a - A B

a - A B = 10 7 P m ←

Passo 4

(5) → (3)

P = 5 2 m 10 7 P m - 3 4 m L α A B

P = 25 7 P - 3 4 m L α A B

- 18 7 P = 3 4 m L α A B

α A B = 24 7 P m M

→ + a A = L 2 α A B - a - A B

= L 2 24 7 P m L - 10 7 P m

a A = 12 7 - 10 7 P m

← + a B = L 2 α A B + a - A B = L 2 24 7 P m L + 10 7 P m

a B = 12 7 + 10 7 P m

Resposta

a A = 2 7 P m →

a B = 22 7 P m ←

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga AE de 2,5m está sendo baixada por dois guindastes. No instante mostrado na figura, sabe-se que a velocidade do ponto D é de 600m m / s para baixo e que a velocidade do ponto E é de 900m m / s p
Um helicóptero desloca-se horizontalmente na direção x a uma velocidade de 200k m / h . Sabendo que as lâminas principais giram no sentido horário com uma velocidade angular de 180r p m , determine o
O carretel de fita e sua estrutura de apoio são puxados para cima com uma velocidade v A = 750m m / s . Sabendo que o carretel de 80 mm de raio tem uma velocidade angular de 15r a d / s no sentido hor
O carretel de fita e sua estrutura de apoio são puxados para cima com uma velocidade v A = 100m m / s . Sabendo que a extremidade B da fita é puxada para baixo com velocidade de 300m m / s e que, no i
Resolva o Problema Resolvido 15.2, considerando que a cremalheira inferior não é fixa, mas se desloca para a esquerda com velocidade de 0,6m / s .