A barra esbelta homogênea tem uma seção transversal uniforme e está dobrada na forma mostrada. Calcule a coordenada y do centro de massa da barra. (Lembrete: O comprimento do arco diferencial é ).
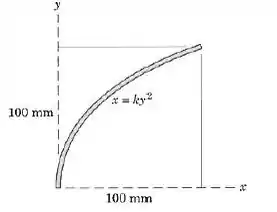
Passo 1
Sabendo que as equações para encontrar o centro de massa da barra é dado por:
Dessa maneira, vamos primeiro encontrar o comprimento do problema.
Passo 2
Mas antes vamos escolher um elemento de comprimento, para assim podermos integrar, com isso:
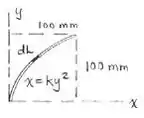
Pronto! Escolhido o elemento de comprimento vamos integrar ele em relação a y e temos o nosso comprimento, de modo que a questão já nos dá uma dica de quem é . Dessa maneira:
Agora precisamos encontrar a função que corresponde a curva, dessa maneira como é um arco, este pode ser descrito por uma parábola,
Desta forma, se derivarmos x em função de y, teremos:
Passo 3
Tendo a função que descreve o nosso problema fica mais fácil de integrar, dessa maneira o comprimento é dado por:
Agora basta resolvermos essa integral que teremos nossa área, sendo assim:
Portanto:
Passo 4
Ante de aplicar a equação para achar o centro de massa na coordenada y, vamos resolver a integral:
Depois é só dividir pela área que teremos o ponto. Logo,
Pronto! Só substituir na equação, se tiver alguma dificuldade na resolução das integrais recomendo que revise o assunto de integrais em cálculo que encontra na própria plataforma. Agora vamos substituir: