Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 05
Uma haste semicircular uniforme de raio é apoiada em um rolamento em sua extremidade superior e está livre para oscilar no plano vertical. Calcule o ângulo formado pelo diâmetro com a vertical para a posição de equilíbrio.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o ângulo que define a posição de equilíbrio do corpo.
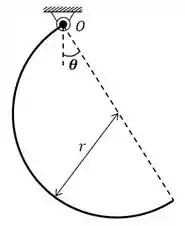
Lembrando que estamos lidando com uma barra, logo utilizaremos aqui as equações de linha.
Vamos analisar primeiro o caso em que e o eixo passando pela origem (apoio):
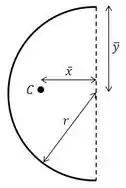
Onde a posição do centroide é obtida pela Tabela D/3 – Propriedades de Figuras Planas:
Passo 2
Show, tendo isso, na situação de equilíbrio do corpo inclinado em , a origem deve estar alinhada com o centroide, ou seja:
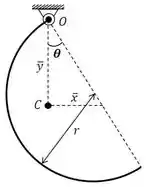
Dessa forma, é dado por:
Bem de boa né?
Ufa! Essa já foi hein? Partiu pra próxima!
