Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 07
A roda de 100 kg tem um raio de giração em relação a seu centro O . Se a roda parte do repouso, determine sua velocidade angular em t = 3 s.
Passo 1
Para a resolução desse exercício, iremos adotar . Primeiramente iremos calcular o momento de inércia da roda em relação ao ponto O:
Passo 2
Agora iremos aplicar o somatório de momento em torno do ponto O com o auxílio da imagem a seguir para obter o valor da aceleração angular:
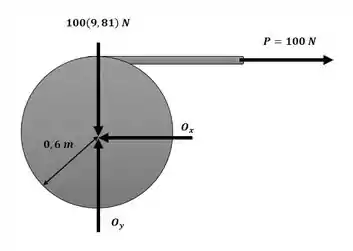
Passo 3
Agora iremos usar a equação da velocidade angular para descobrir a velocidade final da roda:
Resposta
Exercícios de Livros Relacionados
95. O avião a jato na parte inferior de uma acrobacia aérea na forma de um círculo em um plano vertical, tem uma tendência, devido a ação giroscópica do rotor do motor, a mudar de direção para a direi
110. Se a roda no caso (a) do problema 7 / 109 é forçada a executar uma precessão em torno da vertical, por um acionamento mecânico na taxa constante de Ω = 2 j ^r a d / s , determine o momento fletor
A empilhadeira manual tem uma massa de 70 kg e centro de massa em G. Determine a maior aceleração para cima da bobina de 120 kg de maneira que nenhuma reação sobre as rodas exceda 600 N.
113. A haste uniforme de 640m m possui uma massa de 3k g e está soldada em seu centro ao disco circular uniforme com 160m m de raio, que possui uma massa de 8k g . A unidade recebe uma velocidade de g
114. O motor elétrico possui uma massa total de 10k g e é apoiado pelos suportes de montagem A e B presos a plataforma giratória. A armadura do motor possui uma massa de 2,5k g e um raio de giração de