A barra fina de comprimento L e massa m é solta do repouso quando = 0°. Determine como uma função de as forças normal e de atrito que são exercidas pelo degrau sobre a barra em A na medida em que ela cai para baixo. Em qual ângulo a barra começa a deslizar se o coeficiente de atrito estático em A é ?

Agora iremos aplicar as equações do movimento ao sistema com o auxílio da figura a seguir:

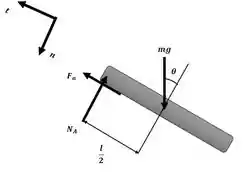
Começando pelo somatório de momentos em torno do ponto A:

Essa será nossa equação número 1. Agora, aplicaremos o somatório de forças na direção tangencial:

Substituindo a equação 1 nessa expressão obteremos a força de reação em A:

Essa será nossa equação número 2. Agora aplicaremos o somatório de forças na direção normal:

Essa será nossa equação número 3.

Agora, iremos lançar mão da equação fornecida no livro:

Substituindo o valor de encontrado na equação 1 e integrando:

Substituindo esse valor na equação número 3, obteremos o valor da força de atrito:

Agora, para obter o ângulo em que a barra começa a deslizar, assumiremos o caso limite, onde:

Sendo assim, substituindo os valores de e já obtidos: