Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 65

Os passageiros, a gôndola e sua estrutura de balanço têm uma massa total 50 Mg, um centro de massa em G e um raio de giração k B = 3,5 m. Adicionalmente, o bloco de aço de 3 Mg em A pode ser considerado como um ponto de massa concentrada. Determine o ângulo θ para o qual a gôndola vai oscilar antes que ela pare momentaneamente, se tem uma velocidade angular de ω = 1 rad/s em seu ponto mais baixo.

Passo 1

Vamos considerar a aceleração da gravidade como g = 9,81   m / s 2 .

Começaremos analisando o momento de inércia da gondola e do contra peso com relação ao ponto B:

I B = m B k B 2 + m a ç o r a ç o 2

I B = 50 10 3 3,5 2 + 3 10 3 3 2

I B = 639,5 10 3 k g . m 2

Passo 2

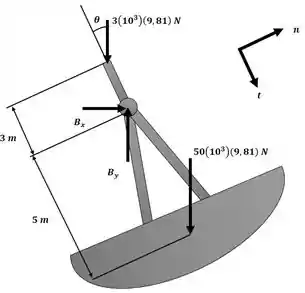
Agora, iremos aplicar o somatório de momentos em torno do ponto B, conforme ilustrado na figura a seguir:

↺ + ∑ M B = I B α

3 10 3 9,81 s e n θ 3 - 50 10 3 9,81 s e n θ 5 = 639,5 10 3 α

α = - 3,697 s e n θ

Passo 3

Tendo conhecimento da relação apresentada no livro:

ω d ω = α d θ

Podemos substituir o valor encontrado para α , integrar e encontrar o valor de θ :

∫ 1 0 ω d ω = ∫ 0 θ - 3,697 s e n θ d θ

E resolvendo as integrais simples:

ω 2 2 1 0 = 3,697 c o s θ 0 θ

θ = 30,1 °

Resposta

θ = 30,1 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . O conjunto inteiro gira em torno do eixo vertical Z na taxa
Se o motor atinge uma velocidade de 3000 rpm em dois segundos a partir do repouso com aceleração constante, determine a aceleração angular total do rotor e do disco 1/3 de segundo após ser ligado, se
O ventilador de 4 pás gira em torno do eixo fixo OB com uma velocidade angular constante de N = 1200 rpm. Escreva as expressões vetoriais para a velocidade v e a aceleração a da extremidade A da pá do
O disco circular está girando em torno do eixo OC com velocidade angular constante ω =20r a d / s . Em um determinado instante, o ponto A sobre a borda passa por um ponto cujas coordenadas x-y-z são 4
A barra é articulada em torno do eixo O-O do garfo, eu está preso à extremidade do eixo vertical. O eixo gira com uma velocidade angular constante ω 0 como mostrado. Se θ está diminuindo na taxa const