Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 62

O pêndulo consiste de uma esfera de 15 kg e uma barra fina de 5 kg. Calcule a reação no pino O logo após a corda AB ser cortada.

Passo 1

Se lembra aquela história do pêndulo ideal? Então aqui não temos isso!!

O pêndulo deste problema é o chamado pêndulo real, e por isso devemos calcular seu momento de inércia para resolver.

Depois de calcular o momento de inércia vamos aplicar algumas equações da dinâmica e “voilá”.

Passo 2

Vamos começar encontrando o valor do momento de inércia da barra, lembrando que a barra rotaciona em torno de uma de suas extremidades, logo o momento de inércia é dado como:

I G B = 1 3 m l 2

I G B = 1 3 5 0,6 2

I G B = 0,6   k g ⋅ m 2

E, agora, o momento de inércia da esfera, aqui vamos ter que usar o teorema dos eixos paralelos então:

I G E = I 0 + m d 2

Onde

I 0 = 2 5 m r 2

I G E = 2 5 m r 2 + m d 2

I G E = 2 5 ⋅ 15 ⋅ 0,3 2 + 15 ⋅ 0,9 2

I G E = 12,69   k g ⋅ m 2

Logo o momento de inércia total é:

I = I G E + I G B

I = 12,69 + 0,6

I = 13,29   k g ⋅ m 2

Passo 3

Agora entra a parte da dinâmica!

No momento em que a corda é cortada, a componente normal (direção horizontal) da aceleração do centro de massa da esfera e da barra são iguais a zero, uma vez que a velocidade angular do pêndulo ω = 0 nesse instante.

Lembrando que a aceleração normal (centrípeta) é:

a c p = v 2 r = ω 2 ⋅ r

Por isso é nula.

Enquanto a aceleração tangencial é:

a t = α ⋅ r

Podemos visualizar a situação com o auxílio da figura a seguir:

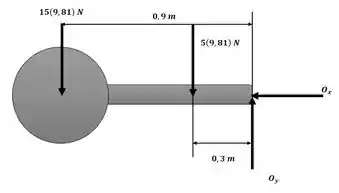
A componente tangencial da aceleração do centro de massa da esfera é dado por:

a G t E = α r E = 0,9 α

Já a componente tangencial da aceleração do centro de massa da barra é dada por:

a G t B = α r B = 0,3 α

Aplicando o somatório de momentos em torno do ponto O, temos:

↺ + ∑ M O = I ⋅ α

Como trata-se de dinâmica, ou seja, movimento, o somatório dos momentos é igual ao momento de inércia vezes a velocidade angular.

15 9,81 0,9 + 5 9,81 0,3 = 13,29 ⋅ α

α = 11,07   r a d / s 2

Passo 4

Agora, iremos aplicar o somatório de forças na direção normal:

+ → ∑ F n = m a G n

O x = 0

E, agora, aplicando o somatório de forças na direção tangencial:

+ ↓ ∑ F t = m a G t = m ⋅ [ d ⋅ α ]

15 9,81 + 5 9,81 - O y = 15 0,9 11,07 + 5 0,3 11,07

O y = 30,15   N

Sendo assim:

F O = O x 2 + O y 2 = 0 2 + 30,15 2 → F O = 30,15   N

Resposta

F O = 30,15   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra dobrada possui uma massa ρ por unidade de comprimento e gira em relação ao eixo z com uma velocidade angular ω . Determine a quantidade de movimento angular H o da barra em relação à origem fi
O rotor do giroscópio está girando na taxa constante p = 100r p m em relação aos eixos x - y - z , no sentido indicado. Se o ângulo γ entre o anel de suspensão e o plano horizontal X - Y é levado a au
A barra esbelta de massa m e comprimento l gira em torno do eixo y como o elemento de um cone circular reto. Se a velocidade angular em torno do eixo y é ω , determine a expressão para a quantidade de
O cone circular reto maciço de massa m , comprimento b , e raio da base r gira a uma velocidade angular p em torno de seu eixo de simetria. Simultaneamente, o suporte e o eixo da haste anexa giram na
A nave espacial mostrada possui uma massa m com centro de massa G . Seu raio de giração em relação a seu eixo z de simetria rotacional é k e em relação a ambos os eixos x ou y é k ' . No espaço, a nav